
The motor of a metro train can give it an acceleration of $1m/s^{2}$ and the brakes can give a negative acceleration to the metro of $3m/s^{2}$. What will be the shortest time which the train can make trips between the two stations $1215\;m$ apart?
\[\begin{align}
& A.60s \\
& B.56.9s \\
& C.58.2s \\
& \text{D}\text{.none of the above} \\
\end{align}\]
Answer
584.7k+ views
Hint: The metro train here undergoes acceleration and retardation, and then clearly it will cover some distance during this process in some time. Then to calculate the time it will take to cover the given distance we can use the equations of motions.
Formula used:
$s=ut+\dfrac{1}{2}at^{2}$ and $v=u+at$
Complete step-by-step solution:
Let us consider that the metro travels in the straight line and is at rest, at A, at time $t=0$ as shown in the figure below. Then let it cover some distance $s_{1}$ to reach B in $t=t_{1}$ due to acceleration $a=1m/s^{2}$.
Let the train travel from B to C in time $t=t_{2}$ to cover a distance $s_{2}$ due to retardation $r=3m/s^{2}$ .
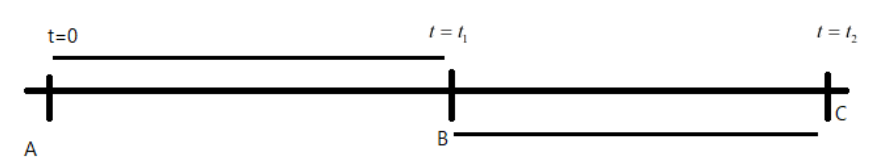
Then from the equation of motions, we know that
$v=u+at$
Since at A the train is at rest, we get $u=0$, also since the trains travels $s=s_{1}$ distance to reach B in $t=t_{1}$ time due to an acceleration $a=1m/s^{2}$.
Then the final velocity $v$ of the train at B is given as :$v=0+1\times t_{1}$
$\implies v=t_{1}$
Also, the distance covered by the train from A to B is given as $s=ut+\dfrac{1}{2}at^{2}$
Then, $s_{1}=0+\dfrac{1}{2}t_{1}^{2}$
$\implies s_{1}=\dfrac{1}{2}t_{1}^{2}$
Now the initial velocity of the train from B to C is $u=t_{1}$, it covers a distance $s_{2}$ in time $t=t_{2}$ time due to an deceleration $r=-3m/s^{2}$.
Then the final velocity $v$ of the train at C is given as :$v=t_{1}-3\times t_{2}$
$\implies t_{1}=3 t_{2}$
Also, the distance covered by the train from B to C is given as $s=ut+\dfrac{1}{2}at^{2}$
Then, $s_{2}=t_{1}t_{2}-\dfrac{1}{2}3t_{2}^{2}$
Also, given that $s_{1}+s_{2}=1215m$
Then, $s_{1}+s_{2}=1215m=\dfrac{1}{2}t_{1}^{2}+t_{1}t_{2}-\dfrac{1}{2}3t_{2}^{2}$
$\implies 1215m=\dfrac{1}{2}\left(9t_{2}^{2}-3t_{2}^{2}\right)+3 t_{2}^{2}$
$\implies 1215=6t_{2}^{2}$
$\implies t_{2}=\sqrt{202.5}s=14.2s$
Then, $t_{1}=3t_{2}=3\times 14.2=42.4s$
Thus the total time taken is given as $t=t_{1}+t_{2}=14.2+42.4=58.6s\approx 59s$
Hence the answer is option \[\text{D}\text{.none of the above}\]
Note: Since the train accelerates for some time and decelerates for some time, we can divide the total distance into two parts, such that during a one-time interval, the train accelerates, and during the other, it decelerates. This simplifies the sum.
Formula used:
$s=ut+\dfrac{1}{2}at^{2}$ and $v=u+at$
Complete step-by-step solution:
Let us consider that the metro travels in the straight line and is at rest, at A, at time $t=0$ as shown in the figure below. Then let it cover some distance $s_{1}$ to reach B in $t=t_{1}$ due to acceleration $a=1m/s^{2}$.
Let the train travel from B to C in time $t=t_{2}$ to cover a distance $s_{2}$ due to retardation $r=3m/s^{2}$ .
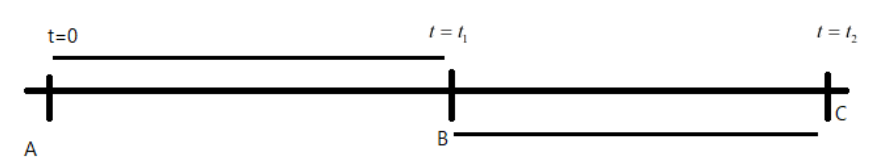
Then from the equation of motions, we know that
$v=u+at$
Since at A the train is at rest, we get $u=0$, also since the trains travels $s=s_{1}$ distance to reach B in $t=t_{1}$ time due to an acceleration $a=1m/s^{2}$.
Then the final velocity $v$ of the train at B is given as :$v=0+1\times t_{1}$
$\implies v=t_{1}$
Also, the distance covered by the train from A to B is given as $s=ut+\dfrac{1}{2}at^{2}$
Then, $s_{1}=0+\dfrac{1}{2}t_{1}^{2}$
$\implies s_{1}=\dfrac{1}{2}t_{1}^{2}$
Now the initial velocity of the train from B to C is $u=t_{1}$, it covers a distance $s_{2}$ in time $t=t_{2}$ time due to an deceleration $r=-3m/s^{2}$.
Then the final velocity $v$ of the train at C is given as :$v=t_{1}-3\times t_{2}$
$\implies t_{1}=3 t_{2}$
Also, the distance covered by the train from B to C is given as $s=ut+\dfrac{1}{2}at^{2}$
Then, $s_{2}=t_{1}t_{2}-\dfrac{1}{2}3t_{2}^{2}$
Also, given that $s_{1}+s_{2}=1215m$
Then, $s_{1}+s_{2}=1215m=\dfrac{1}{2}t_{1}^{2}+t_{1}t_{2}-\dfrac{1}{2}3t_{2}^{2}$
$\implies 1215m=\dfrac{1}{2}\left(9t_{2}^{2}-3t_{2}^{2}\right)+3 t_{2}^{2}$
$\implies 1215=6t_{2}^{2}$
$\implies t_{2}=\sqrt{202.5}s=14.2s$
Then, $t_{1}=3t_{2}=3\times 14.2=42.4s$
Thus the total time taken is given as $t=t_{1}+t_{2}=14.2+42.4=58.6s\approx 59s$
Hence the answer is option \[\text{D}\text{.none of the above}\]
Note: Since the train accelerates for some time and decelerates for some time, we can divide the total distance into two parts, such that during a one-time interval, the train accelerates, and during the other, it decelerates. This simplifies the sum.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




