Question

The motion of a pendulum is an example of:
A. Translatory motion
B. Rotational motion
C. Oscillatory motion
D. Curvilinear motion

Answer 1

Hint: A motion in which a particle undergoes periodic motion is called Simple harmonic motion (S.H.M). Not every periodic motion is S.H.M but every S.H.M is periodic motion. The revolution of earth about the sun is an example of periodic motion but it is not simple harmonic. A motion is said to be simple harmonic only if the acceleration of the particle is the function of first power of displacement and having direction opposite of the displacement.

Complete answer:
Mathematically we can say that if the motion is simple harmonic, it must follow the standard differential equation of simple harmonic motion which is given by $\dfrac{d^2x}{dt^2} = -\omega^2 x$. Let’s consider a bob of mass ‘m’ tied with a string of length ‘l’, pivoted vertically as shown in the figure.

Let’s now displace the bob by a small angle $\theta$, the only force acting on the pendulum is its weight.

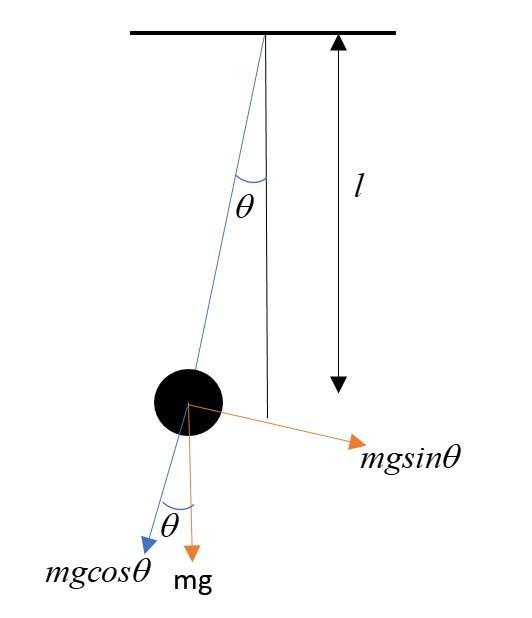
After taking components of the weight, we can see that the only force responsible for the restoring motion of the pendulum is $mgsin\theta$. Thus, writing the equation of motion:
$ma = -mg sin\theta$
Or $a=-gsin\theta$
For smaller angles, $sin \theta \approx \theta$
Thus, $a = -g\theta$
Now, we know that $a_{linear} = r \alpha$, where ‘r’ is the radius in which the body is revolving. So,
$l \alpha = -g \theta$
$\alpha = -\dfrac{g}{l}\theta$
Also, $\alpha = \dfrac{d^2 \theta}{dt^2}$
So $\dfrac{d^2 \theta}{dt^2} = - \dfrac{g}{l}\theta$
Which is the equation of S.H.M. Thus the given motion is simple harmonic. Since simple harmonic motion is an oscillatory motion.

So, the correct answer is “Option C”.

Note:
Students can make mistakes about the fact that every simple harmonic motion is periodic but not every periodic motion is simple harmonic. The revolution of a fan about its own axis is an example of simple harmonic motion. On comparing the obtained equation with the equation of S.H.M, we get a time period of a simple pendulum is $T = 2\pi \sqrt{\dfrac lg}$.