Question

The moment of inertia of a ring about one of its diameter is given as $I$. What will be its moment of inertia about a tangent parallel to the diameter of the ring?

$\begin{align}
 & A.44 \\
 & B.2I \\
 & C.\dfrac{3}{2}I \\
 & D.3I \\
\end{align}$

Answer 1

Hint: Parallel axis theorem should be used in order to solve this question. It states that the moment of inertia of an object about an axis parallel to the axis passing through its centre will be equivalent to the sum of moment of inertia of object about the axis passing through the centre and product of mass of the object times the square of distance between the two axes. This may help you to answer this question.

Complete answer:
First of all, the moment of inertia of a ring about its diameter can be written as,

${{I}_{diam}}=\dfrac{1}{2}M{{R}^{2}}$

Where $M$ be the mass of the ring and $R$ be the radius of the ring.
Here we have to get the moment of inertia of the ring about an axis passing through the tangent of the ring which is parallel to the diameter of the ring.
So from the figure we can see that, the perpendicular distance between the diametrical axis and the tangential axis will be equivalent to the radius of the ring.

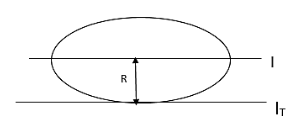
According to the parallel axis theorem which will help us to find the moment of inertia of the body through an axis parallel to the axis passing through the centre. Therefore using these information, we can write that,

${{I}_{T}}={{I}_{diam}}+M{{R}^{2}}$

We know that the moment of inertia of the ring is
${{I}_{diam}}=\dfrac{1}{2}M{{R}^{2}}$
Therefore, we can write that,
$2{{I}_{diam}}=M{{R}^{2}}$
Substituting this in the equation will give,
$\begin{align}
  & {{I}_{T}}={{I}_{diam}}+2{{I}_{diam}} \\
 & =3{{I}_{diam}} \\
\end{align}$

So, the correct answer is “Option D”.

Note:
The parallel axis theorem is also called the Huygens–Steiner theorem. Another name for this is Steiner's theorem. This has been named after Christiaan Huygens and Jakob Steiner respectively.