Question

The mirror image of the focus to the parabola $4\left( x+y \right)={{y}^{2}}$ w.r.t directrix is
(a) (0, 2)
(b) (2, 2)
(c) (– 4, 2)
(d) (– 2, 2)

Answer 1

Hint: In this question, we will first simplify the given equation to a generalized form of parabola ${{\left( y-k \right)}^{2}}=4a{{\left( x-h \right)}}$, and find the focus, the vertex and the equation of the directrix of the parabola. Then, draw the parabola with the obtained data. Now, calculate the distance from the directrix to the focus and move the mirror image by the calculated distance to the left side of the directrix.

Complete step by step answer:
Here, we have been given the equation of parabola, first let us simplify the equation and find the focus of the parabola and the equation of directrix.
$\begin{align}
  & 4\left( x+y \right)={{y}^{2}} \\
 & \Rightarrow 4x+4y={{y}^{2}} \\
 & \Rightarrow 4x={{y}^{2}}-4y
\end{align}$
Now, adding and subtracting 4 on the right-hand side of the equation, we get
$\Rightarrow 4x={{y}^{2}}-4y+4-4$
Now, adding 4 on both the sides of the equation, we get
$\begin{align}
  &\Rightarrow 4x+4={{y}^{2}}-4y+4-4+4 \\
 & \Rightarrow 4\left( x+1 \right)={{y}^{2}}-4y+4
\end{align}$
We can see that, ${{y}^{2}}-4y+4$ is in the form of ${{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}$
Therefore, we will get
$\Rightarrow {{y}^{2}}-2\cdot 2\cdot y+{{\left( 2 \right)}^{2}}=4\left( x+1 \right)$
$\Rightarrow {{\left( y-2 \right)}^{2}}=4\left( x+1 \right)$ ............ (1)
We know, the general form of the parabola is ${{\left( y-k \right)}^{2}}=4a{{\left( x-h \right)}^{2}}$
Now, compare the equation (1) and the general form of the parabola and find the vertex of the parabola $\left( h,\,k \right)$; also find the focus of the parabola $\left( a+h,\,k \right)$ and the equation of the directrix, $x+a-h=0$
Therefore, we get, vertex $\left( h,\,k \right)=\left( -1,\,2 \right)$; $a=1$;
focus $\left( a+h,\,k \right)=\left( 1+\left( -1 \right),\,\,2 \right)$
$\begin{align}
 & =\left( 1-1,\,2 \right) \\
 & =\left( 0,\,2 \right)
\end{align}$
Now, for the equation of the directrix, we get
$\begin{align}
  & x+a-h=0 \\
 &\Rightarrow x+1-\left( -1 \right)=0 \\
 & \Rightarrow x+1+1=0 \\
 & \Rightarrow x+2=0 \\
 & x=-2 \\
\end{align}$
Now, with the help of the equation of directrix, the focus and the vertex of the parabola, let us draw the parabola.

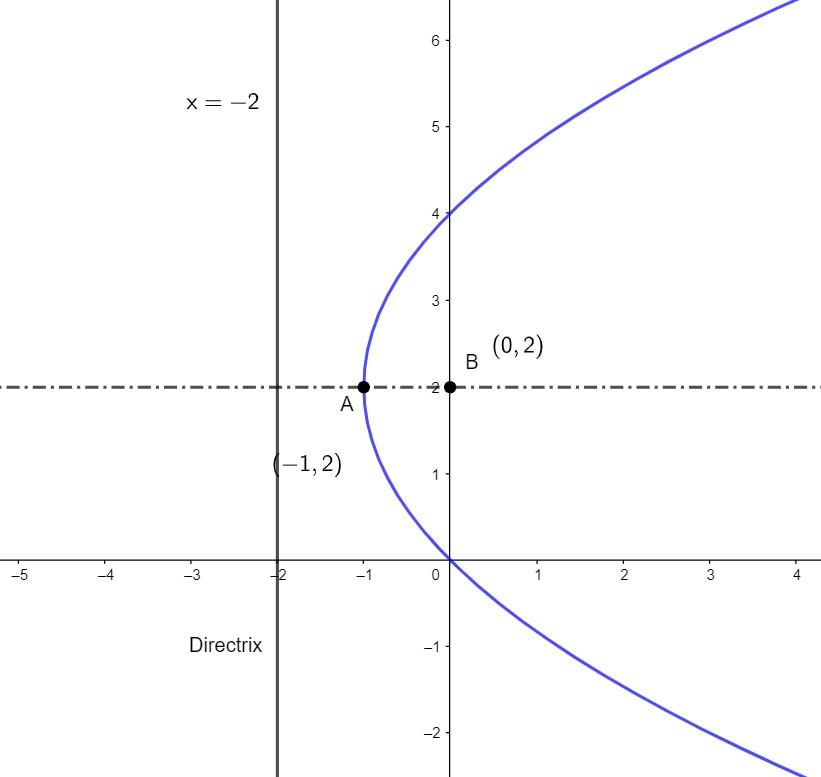
Here from the figure of the parabola, we can see that B (0, 2) is the focus, $x=-2$ is the directrix and $\text{A}\left( -1,\,2 \right)$ is the vertex of the parabola.
Now, we can see that the distance between the focus and the directrix is 2 units. Also, we know that the directrix acts like a mirror, so the mirror image of the focus will be 2 units away from the directrix on the left side of the directrix.
Therefore, from focus to directrix, we get
From 0 to – 2, we move 2 units further, we will get the mirror image of the focus at – 4. Let us show the same in the diagram.

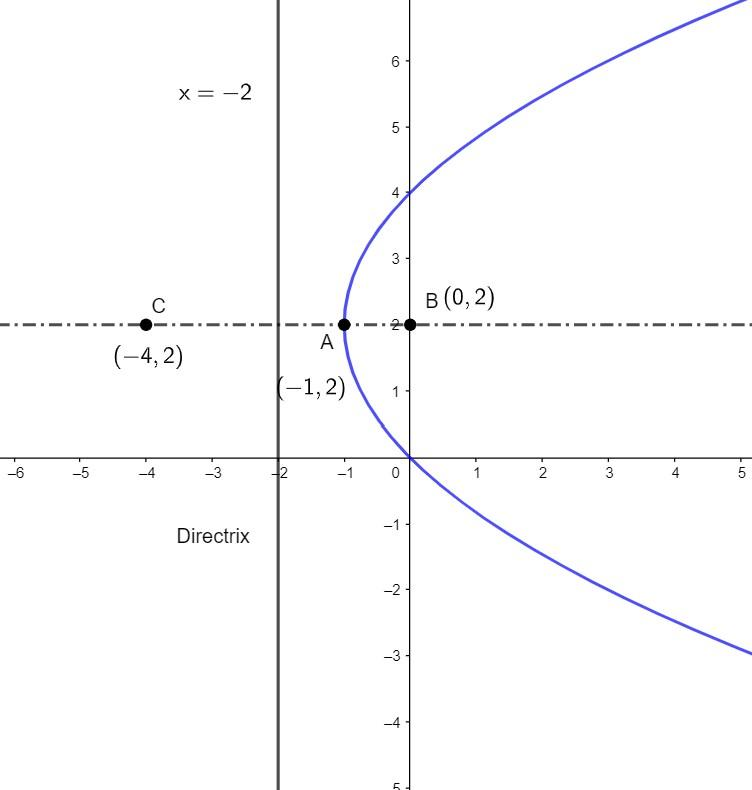
In the above diagram we can see that the mirror image of the focus with respect to the directrix is $\text{C}\left( -4,\,2 \right)$.

So, the correct answer is “Option C”.

Note: A parabola is the locus of a point which moves in a plane such that its distance from a fixed point (focus) is always equal to its distance from a fixed straight line (directrix). Also, a line which is perpendicular to the tangent of the parabola is called the normal to the parabola.