Question

The mirror image of the curve $\arg \left( {\dfrac{{z - 3}}{{z - i}}} \right) = \dfrac{\pi }{6},i = \sqrt { - 1} $in the real axis is:
A.$\arg \left( {\dfrac{{z + 3}}{{z + i}}} \right) = \dfrac{\pi }{6}$
B.$\arg \left( {\dfrac{{z - 3}}{{z + i}}} \right) = \dfrac{\pi }{6}$
C.$\arg \left( {\dfrac{{z + i}}{{z + 3}}} \right) = \dfrac{\pi }{6}$
D.$\arg \left( {\dfrac{{z + 1}}{{z - 3}}} \right) = \dfrac{\pi }{6}$

Answer 1

Hint: Here, we will use the properties of the conjugate of complex numbers for z = a + ib such as $\bar z = a - ib$ and also the property of argument of the complex number like $\arg \left( {\bar z} \right) = - \arg \left( z \right)$ to calculate the mirror image of the given curve.

Complete step-by-step answer:
Here, we are given the curve $\arg \left( {\dfrac{{z - 3}}{{z - i}}} \right) = \dfrac{\pi }{6},i = \sqrt { - 1} $.
The mirror image of any complex number z = a + ib on the real axis is the conjugate of z i. e., $\bar z = a - ib$. It is because when we draw a curve, for example the given curve is a circle and it lies in the 1st quadrant, then its mirror image will lie in the 4th quadrant. The co – ordinate of x – axis will remain the same but the co – ordinate on the y – axis will change its sign.

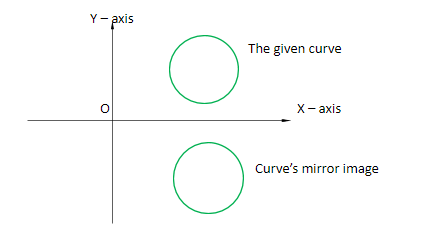
Therefore, the image of z in the real axis is its conjugate $\bar z$.
Now, we have the curve $\arg \left( {\dfrac{{z - 3}}{{z - i}}} \right) = \dfrac{\pi }{6}$
For determining the mirror image of the curve, we will substitute z with $\bar z$in the above equation. After this, we get
$ \Rightarrow \arg \left( {\dfrac{{\bar z - 3}}{{\bar z - i}}} \right) = \dfrac{\pi }{6}$
We know the property of the argument of conjugate of complex numbers i. e., $\arg \left( {\bar z} \right) = - \arg \left( z \right)$. Therefore, using this property in the above equation, we get
$ \Rightarrow \arg \left( {\dfrac{{ - z - 3}}{{ - z - i}}} \right) = \dfrac{\pi }{6}$
$ \Rightarrow \arg \left( {\dfrac{{ - \left( {z + 3} \right)}}{{ - \left( {z + i} \right)}}} \right) = \dfrac{\pi }{6}$
$ \Rightarrow \arg \left( {\dfrac{{z + 3}}{{z + i}}} \right) = \dfrac{\pi }{6}$
Hence, we get the mirror image of the curve $\arg \left( {\dfrac{{z - 3}}{{z - i}}} \right) = \dfrac{\pi }{6},i = \sqrt { - 1} $is found to be $\arg \left( {\dfrac{{z + 3}}{{z + i}}} \right) = \dfrac{\pi }{6}$. Therefore, option(A) is correct.

Note: In such problems, you may get confused amongst the properties used. You can also solve this question using the other property of argument of complex numbers like $\arg \left( {\dfrac{{{z_1}}}{{{z_2}}}} \right) = - \arg \left( {\dfrac{{{z_2}}}{{{z_1}}}} \right)$.