Question

The minute hand of the clock is 14 cm long. How much distance does the end of the minute hand travel in 15 minutes? Use$\left( \pi =\dfrac{22}{7} \right)$
(a) 11 cm
(b) 22 cm
(c) 33 cm
(d) 44 cm

Answer 1

Hint: First, we must draw a clock in the shape of a circle with radius given as 14 cm and also mark the movement of minute hand as 15 minutes from number 12 to 3. Then, by using the concept of the circle which gives the condition that the total angle subtended by the minute hand in 1 hour is ${{360}^{\circ }}$ and by using it we get the angle for 15 minutes. Then, by using the formula for the length L of arc of circular shaped clock where $\theta $ is the angle subtended by minute hand in 15 minutes and r is radius of clock which is given by$L=\dfrac{\theta }{{{360}^{\circ }}}\times 2\pi r$, we get the desired result.

Complete step by step answer:
In this question, we are supposed to find the distance travelled in 15 minutes by the minute hand of the clock when its length is given as 14 cm.
So, before proceeding for this, we must know that the minute hand is large enough that we should consider it as the radius of the clock as the clock is in the shape of a circle.
So, we must draw a clock in shape of circle with radius given as 14 cm and also mark the movement of minute hand as 15 minutes from number 12 to 3 as shown in figure:

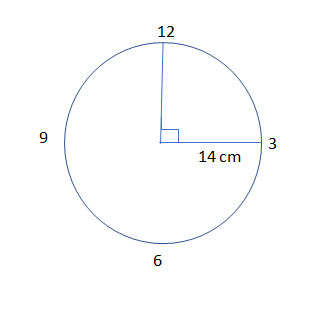
Then, by using the concept of the circle which gives the condition that the total angle subtended by the minute hand in 1 hour is ${{360}^{\circ }}$.
So, by using another concept, that minute hand will go 60 minutes to get an angle of ${{360}^{\circ }}$.
Then, for getting the value of angle for 15 minutes, we have:
$\begin{align}
  & 15\times \dfrac{{{360}^{\circ }}}{60}=15\times {{6}^{\circ }} \\
 & \Rightarrow {{90}^{\circ }} \\
\end{align}$
So, we get the angle subtended by minute hand in 15 minutes as ${{90}^{\circ }}$.
Now, by using the formula for the length L of arc of circular shaped clock where $\theta $ is the angle subtended by minute hand in 15 minutes and r is radius of clock which is given by:
$L=\dfrac{\theta }{{{360}^{\circ }}}\times 2\pi r$
Then, by substituting the values of $\theta $as ${{90}^{\circ }}$and r as 14 cm, we get:
$L=\dfrac{{{90}^{\circ }}}{{{360}^{\circ }}}\times 2\times \dfrac{22}{7}\times 14$
Then, by solving the above expression, we get the desired result as:
$\begin{align}
  & L=\dfrac{1}{4}\times 2\times 22\times 2 \\
 & \Rightarrow L=22cm \\
\end{align}$
So, we get the distance travelled by minute hand in 15 minutes is 22 cm.

So, the correct answer is “Option B”.

Note: Now, in these type questions the only mistake we can occur is the usage of the formula for the length of the arc and confusing it with the formula of the area of the sector. So, in this question the length of that arc is the distance travelled by the minute hand at the circumference of the circle. IF it is asked to find the area A travelled by minute hand is given by:
$A=\dfrac{\theta }{{{360}^{\circ }}}\times \pi {{r}^{2}}$.