Question

The minimum value of the expression cos2x+cosx for real values of x is:
[a] $\dfrac{-9}{8}$
[b] 0
[c] -2
[d] None of these

Answer 1

Hint: Checking for critical points in the intervale $[0,2\pi )$ is sufficient due to periodicity of cos x and cos2x. Differentiate once w.r.t x and put derivative equal to 0 to find the critical points. Use the first derivative test to determine whether a critical point is local maxima or minima.

Complete step-by-step answer:
First derivative test: If f(x) is a continuous and differentiable function and f’(a) = 0, then
[i] If $\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f'\left( x \right)>0$ and $\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f'\left( x \right)<0$, then x = a is a point of local maxima
[ii] If $\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f'\left( x \right)<0$ and $\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f'\left( x \right)>0$, then x = a is a point of local minima
Let f(x) = cos2x+cosx
Differentiating once we get
f’(x) = -2sin2x-sinx = 0
i.e. 2sin2x+sinx = 0
We know that sin2x = 2sinx cosx
Using the above formula, we get
4sinxcosx+sinx = 0
Taking sinx common, we get
sinx(4cosx+1)=0
i.e sinx = 0 or 4cosx + 1 = 0
if sinx = 0 then $x=0,\pi ${Because sinx = 0 when $x=n\pi $ }
if 4cosx +1 = 0 then
$\begin{align}
  & \cos x=\dfrac{-1}{4} \\
 & \Rightarrow x=\pi +\arccos \left( \dfrac{1}{4} \right),\pi -\arccos \left( \dfrac{1}{4} \right) \\
\end{align}$
In finding the above roots, we have used the property $\cos \left( \arccos x \right)=x$ and $\cos \left( \pi -\theta \right)=\cos \left( \pi +\theta \right)=-\cos \theta $.

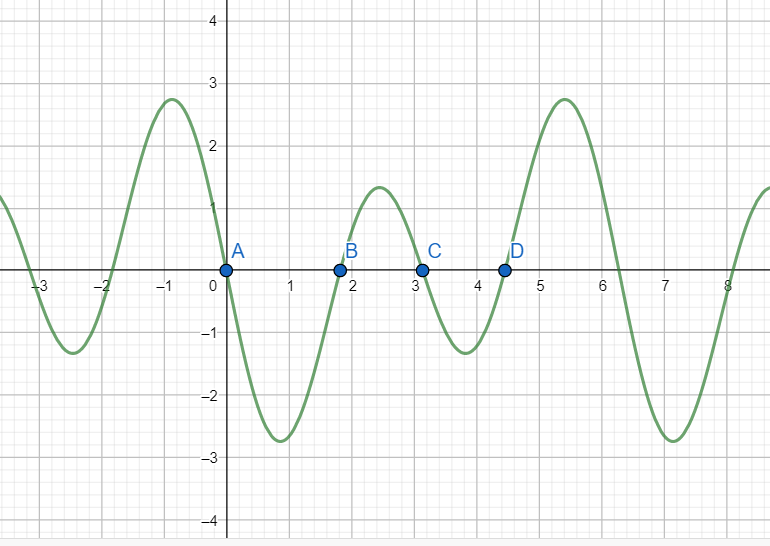
The graph of f’(x) is shown above.
Around point x = 0(Point A in the graph of f’(x)): f’(x) changes sign from +ve to -ve as we move left of 0 to right of 0. Hence, from first derivative test, x = 0 is a point of local maxima
Around point $x=\pi -\arccos \left( \dfrac{1}{4} \right)$(Point B in the graph of f’(x)): f’(x) changes sign from -ve to +ve as we move left of $\pi -\arccos \left( \dfrac{1}{4} \right)$ to the right of $\pi -\arccos \left( \dfrac{1}{4} \right)$. Hence, from the first derivative test, $x=\pi -\arccos \left( \dfrac{1}{4} \right)$ is a point of local minima.
Around point $x=\pi $ (Point C in the graph of f’(x)): f’(x) changes sign from +ve to -ve as we move left of $\pi $ to the right of $\pi $.
Around point $x=\pi +\arccos \left( \dfrac{1}{4} \right)$ (Point D in the graph of f(x)): f’(x) changes sign from -ve to +ve as we move left of $\pi +\arccos \left( \dfrac{1}{4} \right)$ to the right of $\pi +\arccos \left( \dfrac{1}{4} \right)$. Hence $x=\pi +\arccos \left( \dfrac{1}{4} \right)$ is a point of local minima.
Now
 $\begin{align}
  & f\left( \pi -\arccos \left( \dfrac{1}{4} \right) \right)=\cos \left( 2\pi -2\arccos \left( \dfrac{1}{4} \right) \right)+\cos \left( \pi -\arccos \left( \dfrac{1}{4} \right) \right) \\
 & =\cos \left( 2\arccos \left( \dfrac{1}{4} \right) \right)-\cos \left( \arccos \left( \dfrac{1}{4} \right) \right) \\
 & =2{{\cos }^{2}}\left( \arccos \left( \dfrac{1}{4} \right) \right)-1-\dfrac{1}{4} \\
 & =\dfrac{2}{16}-\dfrac{5}{4} \\
 & =\dfrac{-9}{8} \\
\end{align}$
and
$\begin{align}
  & f\left( \pi +\arccos \left( \dfrac{1}{4} \right) \right)=\cos \left( 2\pi +2\arccos \left( \dfrac{1}{4} \right) \right)+\cos \left( \pi +\arccos \left( \dfrac{1}{4} \right) \right) \\
 & =\cos \left( 2\arccos \left( \dfrac{1}{4} \right) \right)-\cos \left( \arccos \left( \dfrac{1}{4} \right) \right) \\
 & =2{{\cos }^{2}}\left( \arccos \left( \dfrac{1}{4} \right) \right)-1-\dfrac{1}{4} \\
 & =\dfrac{2}{16}-\dfrac{5}{4} \\
 & =\dfrac{-9}{8} \\
\end{align}$
Hence the minimum value of the trigonometric expression cos2x+cosx is $\dfrac{-9}{8}$.
Hence option [a] is correct.

Note: Alternative solution:
We know $\cos 2x=2{{\cos }^{2}}x-1$
Hence $\cos 2x+\cos x=2{{\cos }^{2}}x-1+\cos x$
Put $t=\cos x$ we get\[f\left( t \right)=2{{t}^{2}}+t-1,-1\le t\le 1\]
We know the quadratic expression $a{{x}^{2}}+bx+c$ where a>0 attains minima when $x=\dfrac{-b}{2a}$
Since $\dfrac{-b}{2a}=\dfrac{-1}{2\times 2}=\dfrac{-1}{4}$ is in the domain of t.
We have the minimum value of f(x) = minimum value of f(t)
$\begin{align}
  & =2{{\left( \dfrac{-1}{4} \right)}^{2}}+\dfrac{-1}{4}-1 \\
 & =\dfrac{1}{8}-\dfrac{5}{4} \\
 & =\dfrac{-9}{8} \\
\end{align}$
which is the same as obtained above.