Question

The miller indices of the shaded plane shown in the figure below are:

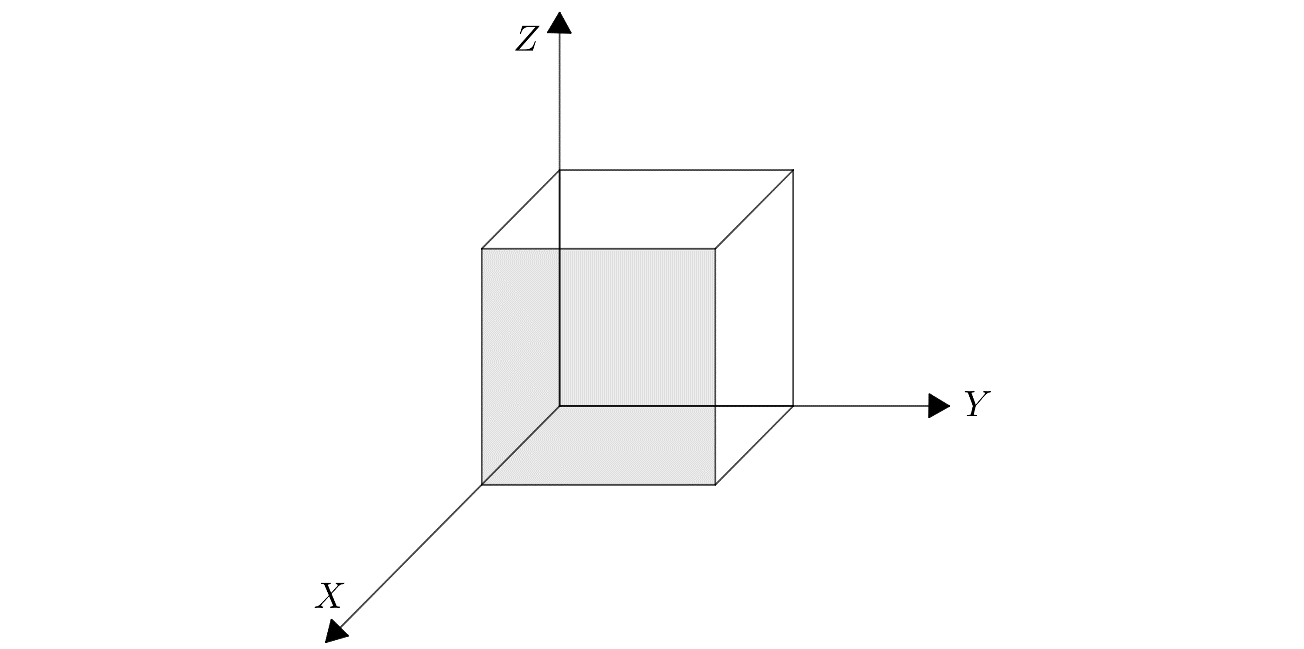
(A) $ \left( 0\;0\;1 \right) $
(B) $ \left( 0\;1\;0 \right) $
(C) $ \left( 0\;1\;1 \right) $
(D) $ \left( 1\;0\;0 \right) $

Answer 1

Hint :Miller indices are used for the vector representation of the orientation of a plane in a crystal lattice. To find the miller indices of the given plane, we will take the intercepts of the plane on each axis, then convert them to fractional coordinates. The reciprocal of the fractional coordinates gives us the required miller indices.

Complete Step By Step Answer:
Miller indices can be defined as a set of three numbers representing the three planes or axes i.e. the $ X-axis $ , the $ Y-axis $ , and the $ Z-axis $ .
Miller indices are used to represent a certain plane or a group of parallel planes formed by the atoms in a crystal lattice.
There is a fixed set of rules to find the miller indices from a given plane. We will understand the rules, and solve it for the particular question.
(1) Find the intercepts of the plane.
Here, we are given a plane which interests the $ x-axis $ at a certain point. Let the point be $ a $ . Hence, the $ x-intercept $ of the given plane is $ a $ .
Now, the plane is parallel to the $ y-axis $ and the $ z-axis $ . Hence, it does not intersect both axes at any point. Hence, we can say for the parallel plane that it intersects the $ y-axis $ and $ z-axis $ at infinity.
Hence, the intercepts of the given plane can be written as $ \left( a\ \infty \ \infty \right) $ , where $ a $ is the $ x-intercept $ , first $ \infty $ is the $ y-intercept $ , and second $ \infty $ is the $ z-intercept $
(2) Specify the intercepts in fractional coordinates
Now, we need to change the obtained intercepts to fractional coordinates by dividing the intercepts by the cell dimension (For example $ a\;b\;c $ )
But we know that for a cubic unit cell, the cell dimension for all the coordinates will be the same and equal to the cell constant $ a $ which is also the $ x-intercept $ .
Hence, the fractional coordinates can be written as $ \left( \dfrac{a}{a}\ \dfrac{\infty }{a}\ \dfrac{\infty }{a} \right) $
The fractional coordinates can be simplified as $ \left( 1\ \infty \ \infty \right) $
(3) Take the reciprocal of the fractional coordinates
Now, we need to take the reciprocal of the fractional coordinates, which can be written as $ \left( \dfrac{1}{1}\ \dfrac{1}{\infty }\ \dfrac{1}{\infty } \right) $
The above coordinates can be simplified as $ \left( 1\ 0\ 0 \right) $
This is the miller indices for the given plane in the figure.
Hence, the correct answer is Option $ (D) $ .

Note :
To verify whether the obtained answer is correct and also to draw a crystal plane from the miller indices, we can remember that if a plane is parallel to a certain axis, then the coordinate of that particular axis will be zero in the miller indices and vice-versa.