Question

The measures of two angles of a parallelogram are in the ratio 3:2. Find the measure of each of the angles of the parallelogram.

Answer 1

Hint: Assume that the measure of one of the adjacent angles is x, and the measure of the adjacent other angle is y. Use the property that opposite angles of a parallelogram are equal and the sum of angles of a quadrilateral is \[360{}^\circ \]. Also, use the fact that the ratio of two adjacent angles is 3:2. Hence form two linear equations in two variables and solve the system to find the values of x and y. Hence find the measures of angles of the triangle.

Complete step-by-step answer:

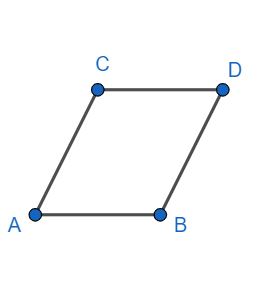
Given: ABCD is a parallelogram. $\angle \text{A:}\angle \text{B::3:2}$
To determine: $\angle \text{A,}\angle \text{B,}\angle \text{C}$ and $\angle \text{D}$
Let $\angle \text{A=}x{}^\circ $ and $\angle \text{B=}y{}^\circ $
Since opposite angles of a parallelogram are equal, we have
$\angle \text{D=}x{}^\circ $ and $\angle \text{C=}y{}^\circ $.
Now we know that the sum of angles of a quadrilateral is equal to \[360{}^\circ \].
Using, we get
\[\begin{align}
  & \angle \text{A+}\angle \text{B+}\angle \text{C+}\angle \text{D=360}{}^\circ \\
 & \Rightarrow x+y+y+x=360 \\
 & \Rightarrow 2x+2y=360 \\
 & \Rightarrow x+y=180\text{ (i)} \\
\end{align}\]

Also, we have $\angle \text{A:}\angle \text{B::3:2}$
Hence, $\dfrac{x}{y}=\dfrac{3}{2}$
Cross multiplying, we get
$2x=3y$
Dividing both sides by 2, we get
$x=\dfrac{3y}{2}\text{ (ii)}$
Substituting the value of x from equation (ii) in equation (i), we get
$\begin{align}
  & \dfrac{3y}{2}+y=180 \\
 & \Rightarrow \dfrac{5y}{2}=180 \\
\end{align}$

Multiplying both sides by $\dfrac{2}{5}$, we get
$\begin{align}
  & \dfrac{5y}{2}\times \dfrac{2}{5}=180\times \dfrac{2}{5} \\
 & \Rightarrow y=72{}^\circ \\
\end{align}$

Substituting the value of y in equation (ii), we get
$x=\dfrac{3}{2}\times 72=108{}^\circ $
Hence the angles of the parallelogram are
$72{}^\circ ,108{}^\circ ,72{}^\circ $ and $108{}^\circ $.

Note: The opposite angles of a parallelogram are equal
Proof:

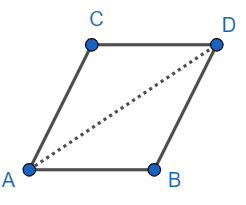
Consider a parallelogram ABCD as shown above. Join AD.
Since CD||AB, we have
$\angle \text{CDA=}\angle \text{DAB (i)}$
Also since DB||AC, we have
 $\angle \text{BDA=}\angle \text{DAC (ii)}$
Adding equation (i) and equation (ii), we get
\[\begin{align}
 & \angle \text{CDA+}\angle \text{BDA=}\angle \text{DAB+}\angle \text{DAC } \\
 & \angle \text{CDB=}\angle \text{CAB } \\
\end{align}\]
Similarly, $\angle \text{ACD=}\angle \text{ABD}$
Hence proved.