Question

The measures of the angles of a triangle are $x+2,x+4\And x+10$ then how do you find the measure of each angle of a triangle?

Answer 1

Hint: We have given the measure of three angles of the triangle and are asked to find the measure of each angle of a triangle. We know that sum of all the three angles of a triangle is ${{180}^{\circ }}$ so we are going to add all the three given angles and then equating the sum of the angles to ${{180}^{\circ }}$. By doing this will give us the value of x and hence will give the measure of each angle of the triangle.

Complete step by step solution:
In the above problem, we have given a triangle with three angles as:
$\left( x+2 \right),\left( x+4 \right)\And \left( 2x+10 \right)$
Now, we are going to draw these angles on to the triangle ABC as follows:

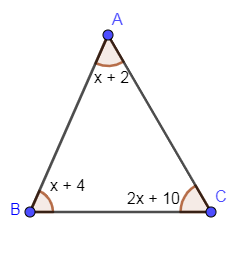
According to properties of a triangle, we know that the sum of all the three angles of a triangle is ${{180}^{\circ }}$.
So, we are going to add all the three angles of the above triangle and then will equate the sum to ${{180}^{\circ }}$.
$x+2+x+4+2x+10={{180}^{\circ }}$
Clubbing the $x$ terms together and the constant terms together in the L.H.S of the above equation we get,
$\Rightarrow 4x+16=180$
Subtracting 16 on both the sides of the above equation and we get,
$\begin{align}
  & \Rightarrow 4x=180-16 \\
 & \Rightarrow 4x=164 \\
\end{align}$
Now, dividing 4 on both the sides of the above equation we get,
$\begin{align}
  & \Rightarrow x=\dfrac{164}{4} \\
 & \Rightarrow x=41 \\
\end{align}$
From the above solution, we got the value of x as 41 so substituting the above value of x in the given angles of the triangle we get,
The angle corresponding to $x+2$ is equal to:
$41+2={{43}^{\circ }}$
The angle corresponding to $x+4$ is equal to:
$41+4={{45}^{\circ }}$
And the angle corresponding to $2x+10$ is equal to:
$2\left( 41 \right)+10=82+10={{92}^{\circ }}$

Hence, we got the three angles of a triangle as ${{43}^{\circ }},{{45}^{\circ }}\And {{92}^{\circ }}$.

Note: We can check whether the measure of the three angles which we got above is correct or not by adding all the three angles and see if the sum is ${{180}^{\circ }}$ or not.
The three angles which we have found above are as follows:
${{43}^{\circ }},{{45}^{\circ }}\And {{92}^{\circ }}$
Adding the above three angles we get,
$\Rightarrow {{43}^{\circ }}+{{45}^{\circ }}+{{92}^{\circ }}={{180}^{\circ }}$
The summation of the three angles will give the value of ${{180}^{\circ }}$ so the angles which we have calculated are correct.