Question

The maximum value of g is
A. At the poles
B. At the top of the Mount Everest
C. At the equator
D. Below the sea level

Answer 1

Hint: Here, the effect of centrifugal acceleration will act on. It’s an acceleration that acts outwards from Earth’s surface. It has different values at different longitudes. It usually tries to reduce the gravitational acceleration.

Formula used: $g \prime= g-mR\omega^2.\cos^2\theta$

Complete step-by-step solution:
One has to know the effective value of the acceleration due to gravity at different longitudes. Now, let $\theta$ be the longitude of some place on Earth. Try to imagine a circular plane perpendicular to the axis of Earth along this place. The radius of this circular plane is $R.\cos\theta$. Here R is the radius of Earth and $\theta$ is the longitudinal angle.

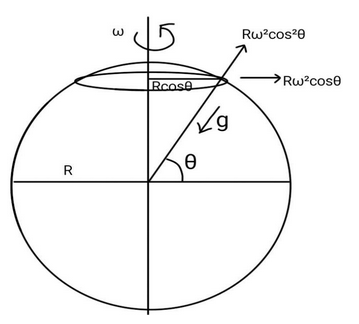
So, the centrifugal acceleration in this place of Earth is given by,
$a_c=R.\cos\theta .\omega^2 $
Here, $\omega$ is the angular velocity of Earth.
Now, component of this acceleration along the direction of g is given by,
$a_c.\cos\theta=R.\omega^2.\cos^2\theta $
This acceleration acts opposite to the acceleration due to gravity. Hence the effective value of g is given by,
$g \prime= g-mR\omega^2.\cos^2\theta$
Now, at the equator, the longitude is zero. So $g \prime$ is very low. But at the poles, $\theta=90^\circ$. So, $g \prime$ is the maximum.
Again, while considering heights, value of g decreases with height as well as with the depth. So, only option A is the correct answer.
Additional information: If a body rotates with angular velocity $\omega$ in a orbit of radius r, its centrifugal acceleration is given by,
$r. \omega^2=\dfrac{v^2}{r}$
Here, v is the linear velocity of the body.

Note: A few things to keep in mind are...
1. While trying to remember the formula, don’t replace cosine with sine. Then you will get the wrong answer.
2. Remember that, centrifugal acceleration always works in the outward direction.
3. Angular velocity of Earth is constant on all the places of Earth.