Question

The maximum tension that an inextensible ring of radius 1m and mass density 0.1kg/m can bear is 40N. The maximum angular velocity with which it can be rotated in a circular path is
(A) 20 rad/s
(B) 18 rad/s
(C) 16 rad/s
(D) 15 rad/s

Answer 1

Hint: We first need to find the force that a small part of the ring of mass $ dm $ exerts while moving in the circular motion. This force will be equal to the sine component of the tension as the cosine component will cancel out. So by equation this value, we can find the maximum angular velocity due to the maximum tension.

Formula used: In this solution, we will be using the following formula,
 $\Rightarrow F = m{\omega ^2}r $
where $ F $ is the centripetal force on the mass $ m $, $ r $ is the radius of the circular motion and $ \omega $ is the angular velocity.

Complete step by step solution:
In the question, the ring is given as in the figure having a radius $ r $ and rotating with the angular velocity $ \omega $ . We consider a small part of the ring of mass $ dm $ as in the figure.

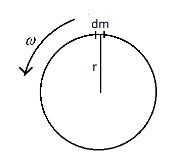
Now for the mass $ dm $ , it subtends an angle $ d\theta $ with the radius and there is a tension that acts on in the tangential direction in both the sides. So we can redraw the tension on the mass $ dm $ as,

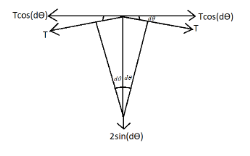
Therefore as from the figure we can see that the tension can be broken down into 2 perpendicular components. The cosine component of the tension cancels each other out because they are in opposite directions. But the sine components being in the same direction gets added. Hence we get a force of $ 2T\sin \left( {d\theta } \right) $ that is acting radially inward.
Now, due to this small mass $ dm $ , the centripetal force acting on the mass in the radial direction is given by, $ F = \left( {dm} \right){\omega ^2}r $
Now this force is equal to the sine component of the tension force. So equating them we get
 $\Rightarrow 2T\sin (d\theta ) = \left( {dm} \right){\omega ^2}r $
In the question, we are given the mass density of the ring as $ \lambda $ . So the mass of the small part $ dm $ is given by
 $\Rightarrow dm = \lambda \times 2rd\theta $
So substituting this value we get
 $\Rightarrow 2T\sin (d\theta ) = \lambda 2r\left( {d\theta } \right){\omega ^2}r $
The value of $ \sin \theta $ will be equal to $ \theta $ for a small value of $ \theta $ .
So we get $ 2T(d\theta ) = \lambda 2\left( {d\theta } \right){\omega ^2}{r^2} $
Therefore, the $ 2d\theta $ will be cancelled out from both the sides. Hence, we will get
 $\Rightarrow T = \lambda R{\omega ^2}{r^2} $
So, from this the value of the angular velocity will be,
 $\Rightarrow {\omega ^2} = \dfrac{T}{{\lambda {r^2}}} $
On taking square root on both the sides we will get,
 $\Rightarrow \omega = \sqrt {\dfrac{T}{{\lambda {r^2}}}} $
For the maximum tension in the question it is given $ T = 40N $ , the radius of the ring is $ r = 1m $ and the mass density $ \lambda = 0.1kg{m^{ - 1}} $ . Therefore, the maximum angular velocity is,
 $\Rightarrow {\omega _{\max }} = \sqrt {\dfrac{{40}}{{0.1 \times {{\left( 1 \right)}^2}}}} $
On calculation we get,
 $\Rightarrow {\omega _{\max }} = \sqrt {\dfrac{{40 \times 10}}{1}} $
Hence the maximum angular velocity is,
 $\Rightarrow {\omega _{\max }} = 20rad/s $
So the correct answer will be option A.

Note:
The centripetal force on the ring is the force that makes it move in the curved circular path. The direction of the centripetal force is always in the radial direction. Its value is given by, $ F = \dfrac{{m{v^2}}}{r} $ . Now since $ v = \omega r $ . So we can write, $ F = \dfrac{{m{{\left( {\omega r} \right)}^2}}}{r} $
Which gives us,
 $\Rightarrow F = \dfrac{{m{\omega ^2}{r^2}}}{r} $ . So on cancelling the $ r $ on numerator and denominator we get,
 $\Rightarrow F = m{\omega ^2}r $ .