Question

The maximum range of bullet fires from a toy pistol mounted on a car at rest is \[{R_ \circ } = 40m\].What will be the acute angle of inclination of the pistol for maximum range when the car is moving in the direction of firing with uniform velocity \[v = 20\dfrac{m}{s}\], on a horizontal surface? \[\left( {g = 10\dfrac{m}{{{s^2}}}} \right)\]
(A) \[{30^ \circ }\]
(B) \[{60^ \circ }\]
(C) \[{75^ \circ }\]
(D) \[{45^ \circ }\]

Answer 1

Hint: In this question, we need to determine the acute angle of inclination of the pistol for maximum range such that the car is moving in the direction of firing with uniform velocity. For this, we will use the equations of the projectile motions which is the special case of the linear motions.

Complete step by step answer:
Maximum range of bullet fired \[{R_ \circ } = 40m\]
uniform velocity of the car \[v = 20\dfrac{m}{s}\]
We know the range of a projection of a particle is given by the formula
\[ \Rightarrow R = \dfrac{{{u^2}}}{g}\ operator\,name {Sin} 2\theta \]
Where the range of a projection of a particle will be maximum if angle of projection is maximum
i.e. \[\theta = {90^ \circ }\], hence the formula for maximum projection becomes
\[{R_{\max }} = \dfrac{{{u^2}}}{g} - - (i)\]
Now since the maximum projection of bullet is given so the velocity of toy pistol
\[
{R_{\max }} = \dfrac{{{u^2}}}{g} \\
\Rightarrow 40 = \dfrac{{{u^2}}}{{10}} \\
\Rightarrow{u^2} = 400 \\
\Rightarrow u = 20\dfrac{m}{s} - - (ii) \\
\]
Now it is said that the car stats moving in the direction of firing with uniform velocity \[v = 20\dfrac{m}{s}\]

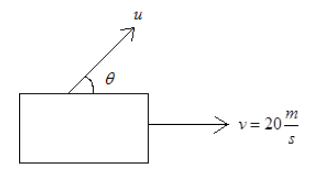
Now since the car is moving in x direction and the bullet is also fired in x direction so the total speed becomes
\[u_{_x}^1 = 20 + u\cos \theta - - (iii)\]
\Rightarrow\[{u_y} = u\sin \theta - - (iv)\]
Now we know the maximum range of projection is given as
\[R = \dfrac{{2 \cdot {u_x} \cdot {u_y}}}{g} - - (v)\]
Hence by substituting the values from equation (iii) and (iv), we get
\[R = \dfrac{{2 \cdot \left( {20 + u\cos \theta } \right) \cdot \left( {u\sin \theta } \right)}}{g} - - (vi)\]
Now to maximize the range of projection we can write \[\dfrac{{dR}}{{d\theta }} = 0\]
Hence for maximum range differentiate equation (v) w.r.t. \[\theta \], hence we get
\[
\dfrac{{d\left( {\dfrac{{2\left( {20u\sin \theta + {u^2}\sin \theta \cos \theta } \right)}}{g}} \right)}}{{d\theta }} = 0 \\
\Rightarrow\dfrac{2}{g}\dfrac{{d\left( {20u\sin \theta + {u^2}\sin \theta \cos \theta } \right)}}{{d\theta }} = 0 \\
\Rightarrow\dfrac{2}{g}\left\{ {20\dfrac{d}{{d\theta }}\left( {u\sin \theta } \right) + \dfrac{d}{{d\theta }}\left( {{u^2}\sin \theta \cos \theta } \right)} \right\} = 0 \\
\]
Hence by differentiating we get
\[
\dfrac{2}{g}\left\{ {20\dfrac{d}{{d\theta }}\left( {u\sin \theta } \right) + \dfrac{d}{{d\theta }}\left( {{u^2}\sin \theta \cos \theta } \right)} \right\} = 0 \\
\Rightarrow\dfrac{2}{g}\left\{ {20\left( {u\cos \theta } \right) + {u^2}\dfrac{d}{{d\theta }}\left( {\sin \theta \cos \theta } \right)} \right\} = 0 \\
\]
Now by applying uv rule we can further differentiate the equation as
\[20\left( {u\cos \theta } \right) + {u^2}\left( {{{\cos }^2}\theta - {{\sin }^2}\theta } \right) = 0\]
Now since \[{\sin ^2}\theta + {\cos ^2}\theta = 1\], hence we can further write the equation as
\[20\cos \theta + u\left( {2{{\cos }^2}\theta - 1} \right) = 0\]
This can be written as
\[20\cos \theta + 2u{\cos ^2}\theta - u = 0\]
Now since \[u = 20\dfrac{m}{s}\] from equation (ii), hence we can write
\[
\cos \theta + 2{\cos ^2}\theta - 1 = 0 \\
\]
This is equal to \[2{\cos ^2}\theta + \cos \theta - 1 = 0\]
Hence we get the equation in quadratic form where \[\cos \theta = {60^ \circ },{270^ \circ }\].

Hence acute angle of inclination of the pistol for maximum range when the car is moving in the direction of firing \[{60^ \circ }\]. So,option B is correct.

Note: Sometimes vectors are not aligned on the x-axis or the y-axes and so, they increase the confusion while solving the questions. Always try to simplify the vectors along the x-axis (horizontal) and the y-axis (vertical) and then, do the algebraic operations on the same.