Question

The maximum number of sets obtainable from A and B by applying union and difference operations is
A) 5
B) 6
C) 7
D) 8

Answer 1

Hint:
To calculate maximum numbers of sets obtainable from A and B by applying union and different operations. We draw Vann’s diagram of set A and set B, In the Vann diagram firstly we consider a universal set ‘U’ which is represented by a rectangle, and then we considered its two subsets A and B, With the help of these diagrams, we can calculate the number of sets from by union and intersection of A and B.

Complete step by step solution:
The Venn diagram is given
 

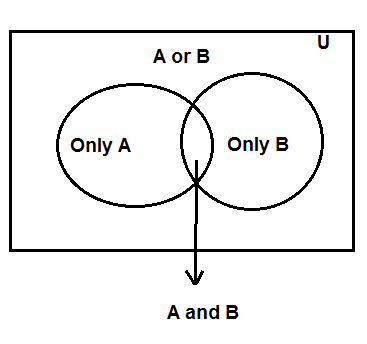
This is the Venn diagram of A and B. There are mainly three areas in the diagram.
Firstly, $ A - B $ represents the set in which there are the elements of A but not B.
Secondly $ A \cup B $ .
It is called A union B. AUB represents the set in which there are all elements of A together with elements of B. In $ A \cup B $ , there are no repeated elements.
Third is $ B - A $
 $ B - A $ represents the set in which there are the elements of set A bit not set B.
Any other set obtained from these two areas either contains or does not contain each area. Therefore, there are a maximum number of $ {2^3} = 2 \times 2 \times 2 = 8 $ possible sets.
These possible sets are A, B, $ A - B $ , $ B - A $ , $ A \cap B $ , others are AUB, A-A and $ (A - B) \cap (B - A) $
Here, A-A is the empty set. The empty set is those sets that do not contain any elements.
Also $ A \cup B $ = $ (A \cap B) \cup (A - B) \cup (B - A) $
So, the total number of sets obtained from the union, and the difference between A and B is 8.

So, option D is correct.

Note:
Here A $ \cap $ B is called A intersection B. Intersection of two sets A and B is the setting in which there are common elements of A and B.
AUB is called the union of A and B. Union of two sets A and B is the setting in which there are the elements of A together with elements of B.
Universal set:- If all the sets under consideration are the sub-set of a fixed set then this fixed set is called a universal set.