Question

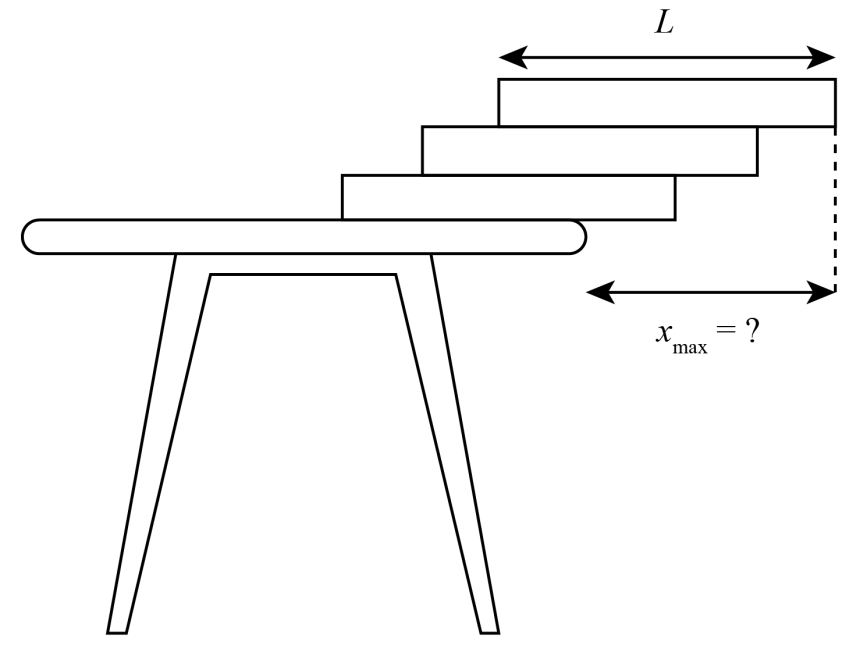
The maximum length that three playing cards can protrude on a table edge?

(A). $\dfrac{L}{{10}}$
(B). $\dfrac{{3L}}{4}$
(C). $\dfrac{{3L}}{{12}}$
(D). $L$

Answer 1

Hint: The physical principle here is to balance the torque (or moments) on the two sides of the table’s edge. The torque on each side is the product of the mass on that side and the distance from its center of mass to the edge.

Complete step by step answer:
Let the mass of each card be $m$. We can first analyze the top two cards. Then the force applied by the top card on the underneath is ${F_1}$ , which will be equal to $mg$, where $g$ is the acceleration due to gravity. When two forces balance one another with no offset, there is no torque, or moment, twisting the block. It is stable. It’s possible to slide the block towards the edge of the table, and provide the centre of mass to remain over the table, then the block is stable. If the centre of mass moves beyond the edge of the table there is no way its weight can be reacted without a moment and the block will topple off the end.For the cards not to topple, the net torque should be equal to zero. Thus, we have,
${F_1}{y_1} = mg\left( {\dfrac{L}{2} - x} \right)$
Torque by contact force at the taken values from zero to $mg\left( {L - x} \right)$ depends on $y$. And hence we have, ${F_1}{y_1} = 0$. So this further implies that,
$
0 = mg\left( {\dfrac{L}{2} - x} \right)\\
\Rightarrow {x_1} = \dfrac{L}{2}
$
Now we can consider three card systems. Here the force will be ${F_2} = 2mg$. For rotational equilibrium,
$
mg{x_2} + 2mg{y_2} = mg\left( {\dfrac{L}{2} - {x_2}} \right)\\
\Rightarrow 2mg{y_2} = mg\left( {\dfrac{L}{2} - 2{x_2}} \right)\\
\Rightarrow {x_2} = \dfrac{L}{4}
$
Similarly we can obtain the relation, for ${x_3}$ as,
${x_3} = \dfrac{L}{6}$
Therefore the total is,
${x_1} + {x_2} + {x_3} = \dfrac{L}{2} + \dfrac{L}{4} + \dfrac{L}{6} = \dfrac{{11L}}{{12}}$

So, the correct answer is “Option B”.

Note:
The moment of the combined centre of mass of the entire loops of cards, around the lower right corner is equal to the sum of the moments of the individual cards. Since the moment of the top card passes directly through this chosen origin, it is zero.