Question

The mass of the bucket full of water is 15 kg. It is being pulled up from a 15 m deep well. Due to hole in the bucket 6 kg water flows out of the bucket. The work done in drawing the bucket out of the well will be \[(g=10m{{s}^{-2}})\]
A. 900 J
B. 1500 J
C. 1800 J
D. 2100 J

Answer 1

Hint: In this case, we can find out the ratio of leakage of water. Then we can find the mass of the bucket at a particular time. We can use this to find the work done at that particular instant. Then we can integrate the work done to find the total work done during the lifting of the bucket.

Formula used:
\[W=mgh\], where m is the mass, g is the acceleration due to gravity and h is the height.

Complete step by step answer:

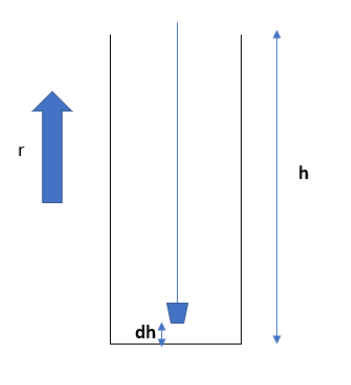
Here, we are trying to lift the bucket with water. Since it has leakage the mass of the bucket will reduce if we are trying to lift. When it reaches on the top, it will lose 6 kg of water. We can assume the elimination of water through the hole at a constant rate. In our case, the change in mass is 6 kg when the bucket is pulled up for 15 metres. Therefore the rate of leakage can be written as,
\[r=\dfrac{6}{15}kg{{m}^{-1}}\]
Throughout the process, the water flows out of the bucket. So, we can consider an instant of time. At that time, the bucket is lifted for a small height (dh).
Then, the mass of the bucket at any instant will be,
\[\text{Mass at a particular time = Total mass - (flow rate }\times \text{ height)}\]
\[\Rightarrow 15-\left[ \dfrac{6}{15}\times h \right]\], since the water is reducing from the bucket.
We can calculate the work done in this instant of time. At that time the height will be dh and work done will be dW.
\[W=mgh\], where m is the mass, g is the acceleration due to gravity and h is the height.
\[dW=\left( 15-\left[ \dfrac{6}{15}\times h \right] \right)gdh\]
To find the total work done throughout the process, we can integrate the dW from 0 to 15.
\[dW=\int\limits_{0}^{15}{\left( 15-\left[ \dfrac{6}{15}\times h \right] \right)gdh}\]
\[W=\left( 15gh-\left[ \dfrac{6}{15}\times g\times \dfrac{{{h}^{2}}}{2} \right]_{0}^{15} \right)\]
\[W=\left( (15\times 10\times 15)-\left[ \dfrac{6}{15}\times 10\times \dfrac{{{15}^{2}}}{2} \right] \right)\]
\[W=1800J\]
So, the total work done to lift the bucket of water is 1800 J. Therefore, the correct option is C.

Note: Here we are finding the work done to lift the bucket. So we can’t find the work done only with the change in mass. We have to find the difference between the total work done and the relaxation that we are getting due to the leakage of water. The negative sign is coming because the water goes out of the system. If we are adding water to the bucket, we have to find the sum of work done.