Question

The mass of an elevator is 4000 kg. Starting from rest how much distance will it rise in 2s if the tension in the cable is 56 kN?
A) 3 m
B) 4 m
C) 8 m
D) 16 m

Answer 1

Hint: We need to find the relation between the mass of the lift, the tension acting on the cable, and the height traveled by the lift under the given conditions. We can use the equations of motion to find the solution for the given problem very easily.

Complete step-by-step solution
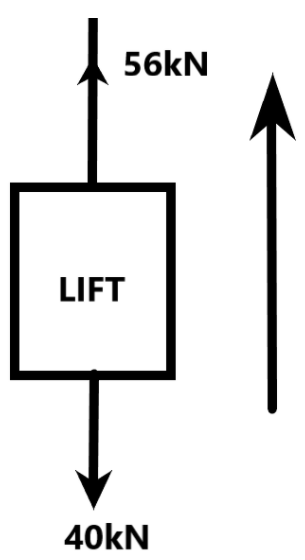
We are given a system of a lift, which is pulled upward by a force of 56kN as it is the tension experienced by the cable. The mass of the lift is given as 4000 kg. We know that the force acting on the lift will be the difference between the force due to the gravitational force and the force exerted by the cable. The net force experienced by the lift in this condition can be given as –
\[\begin{align}
  & {{F}_{net}}=Tension-{{F}_{weight}} \\
 & \Rightarrow {{F}_{net}}=56000-40000 \\
 & \therefore {{F}_{net}}=16000N \\
\end{align}\]

Now, we can find the acceleration possessed by the lift due to this force acting on it as –
\[\begin{align}
  & {{F}_{net}}=ma \\
 & \Rightarrow a=\dfrac{{{F}_{net}}}{m} \\
 & \Rightarrow a=\dfrac{16000}{4000} \\
 & \therefore a=4m{{s}^{-2}} \\
\end{align}\]
Now, we can apply the equation of motion to find the height attained buy the lift in 2 seconds time as –
\[\begin{align}
  & S=ut+\dfrac{1}{2}a{{t}^{2}} \\
 & \Rightarrow h=(0)t+\dfrac{1}{2}(4){{(2)}^{2}} \\
 & \therefore h=8m \\
\end{align}\]
The height attained by the lift in 2 seconds is 8 meters. The correct answer is option C.

Note: We find the net force by finding the difference between the tension on the cable and the weight of the lift. This is because the two forces acting in the opposite directions are therefore canceled in the whole process. For a descending lift, we can sum the forces.