Question

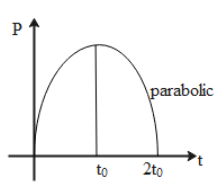
The magnitude of the momentum of a particle varying with time is shown in the figure. The variation of force acting on the particle is shown as:

A.

B.

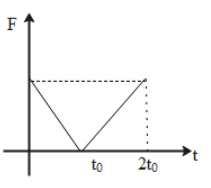
C.

D.

Answer 1

Hint: The momentum of a body is the product of mass and the velocity of the body with which it is moving. According to the law of conservation of momentum, the value of initial momentum is always equivalent to the value of the final momentum. It is denoted by a symbol $P$. The rate of change of momentum is known as force.

Complete answer:
The product of mass and the velocity of the body with which it is moving is known as momentum.
$P=m\times v\quad .....(1)$
So from the graphical representation mention in the question,

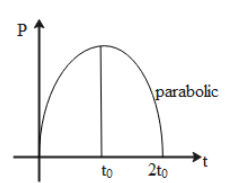
The equation of a parabola is,
$\begin{align}
  & P=at-b{{t}^{2}} \\
 & \Rightarrow at-b{{t}^{2}}=0 \\
\end{align}$
So the above equation we can say that
$\begin{align}
  & t=\dfrac{a}{b} \\
 & a=2{{t}_{0}}b\quad .....(2) \\
\end{align}$
The product of mass and the acceleration with which it is moving is known as force.
$F=m\times a$
With the reference to the equation (1), the above equation can be also represented as,
$\begin{align}
  & F=\dfrac{m\times v}{t} \\
 & \Rightarrow F=\dfrac{dP}{dt} \\
\end{align}$
So, by differentiating the equation of the parabola with rest to the time,
$F=a-2bt$
Using equation (2),
$F=2{{t}_{0}}b-2bt$
Now we can say that,
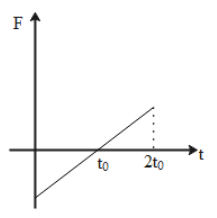
At $t=0$ the value of force will be,
$\begin{align}
  & F=2{{t}_{0}}b-2b(0) \\
 & \Rightarrow F=2{{t}_{0}}b \\
\end{align}$
 At $t={{t}_{0}}$ the value of force will be,
$\begin{align}
  & F=2{{t}_{0}}b-2{{t}_{0}}b \\
 & \Rightarrow F=0 \\
\end{align}$
At $t=2{{t}_{0}}$ the value of force will be,
$\begin{align}
  & F=2{{t}_{0}}b-2b(2{{t}_{0}}) \\
 & \Rightarrow F=-2{{t}_{0}}b \\
\end{align}$
When we plot the graphical representation of the obtained values of the force concerning the increasing time the plot will be as shown in the graph,

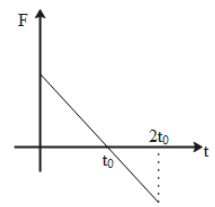
Thus, the correct option which represents the correct graphical representation of force concerning the time for the changing momentum mentioned in the question is Option C.

Note:
Every object in this universe which is in motion or at rest has some momentum. To change the momentum of the body an external force has to be applied to the body. It is hard to control a body that is moving with its maximum momentum.