Question

The magnification of the image when an object is placed at a distance x from the principal focus of a mirror of focal length f is:
A. $\dfrac{x}{f}$
B. $1+\dfrac{x}{f}$
C. $\dfrac{f}{x}$
D. $1-\dfrac{f}{x}$

Answer 1

Hint: We are given that the object is at a distance $x+f$ from the mirror. Using the mirror formula obtains the image distance in terms of the focal length f and the object distance $x+f$. Then, using the fact that magnification is the ratio of the image distance to the object distance, substitute the expressions for the image and object distances that we have obtained to finally arrive at the required relation.
Formula used:
Mirror formula: $\dfrac{1}{f}=\dfrac{1}{u}+\dfrac{1}{v}$
Magnification $M = \dfrac{v}{u}$

Complete answer:
We are given that the object is placed at a distance $x$ from the principal focus $f$ of the mirror. This means that the object is at a distance $u = -(x+f) $ from the mirror. The negative sign indicates that the object is on the side of the reflecting surface of the mirror.

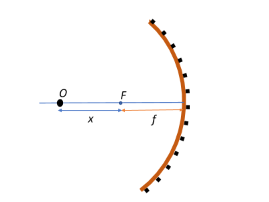
The mirror formula is given as:
$\dfrac{1}{f}=\dfrac{1}{u}+\dfrac{1}{v}$, where $v$ is the image distance from the mirror.
Substituting $u = -(x+f)$ and $f=-f$ in the mirror formula:
$\dfrac{1}{-f} = \dfrac{1}{-(x+f)}+\dfrac{1}{v}$
$\dfrac{1}{v} = -\dfrac{1}{(x+f)} +\dfrac{1}{f} = \dfrac{-f + (x+f)}{(x+f)f} = \dfrac{x}{f(x+f)}$
$\Rightarrow v = \dfrac{f(x+f)}{x}$
Now, the magnification of a mirror is given as :
$M = \dfrac{v}{u}$
$\Rightarrow M = \dfrac{\left(\dfrac{f(x+f)}{x}\right)}{(x+f)} = \dfrac{f(x+f)}{x(x+f)}= \dfrac{f}{x}$

So, the correct answer is “Option C”.

Note:
In general, magnification is expressed in terms of a number preceded by a sign. The sign indicates whether the image is upright or inverted whereas the number indicates if the image is diminished in size or magnified.
$ Magnification = \dfrac{apparent(image) size}{true(object) size}$
If it is > 1 it means that the image is magnified whereas if it is between 0 and 1 the image is minified.
Therefore, total magnification is given by
$Magnification_{resultant} = \pm Magnification$
According to our above chosen convention if it is “+” it means that the image is upright whereas if it is “-“ the image is inverted.