Question

The magnetic flux through the cross-section of the toroidal solenoid is,

(A) $ \dfrac{{{\mu _0}{N_i}h}}{{2\pi }} $
(B) $ \dfrac{{{\mu _0}{N_i}h\left( {b - a} \right)}}{{2\pi r}} $
(C) $ \dfrac{{{\mu _0}{N_i}h}}{{2\pi }}{\log _e}\dfrac{b}{a} $
(D) $ \dfrac{{{\mu _0}{N^2}_ih}}{{2\pi }}{\log _e}\dfrac{a}{b} $

Answer 1

Hint To find out the magnetic flux through the cross-section of the toroidal solenoid, we need to use the Ampere’s circuital law. It is applied to find out the total magnetic field strength in a current carrying conductor.

Formula Used: In this solution we will be using the following formula,
 $\Rightarrow \int {B.dl = N{\mu _0}i} $
where $ B $ is the magnetic field, $ N $ is the number of turns, $ {\mu _0} $ is the permeability in free space and $ i $ is the current.

Complete step by step answer
According to the Ampere’s circuital law, the closed line integral of magnetic field around a current carrying conductor is equal to absolute permeability times the total current threading the conductor.
 $\Rightarrow \int {B.dl = N{\mu _0}i} $
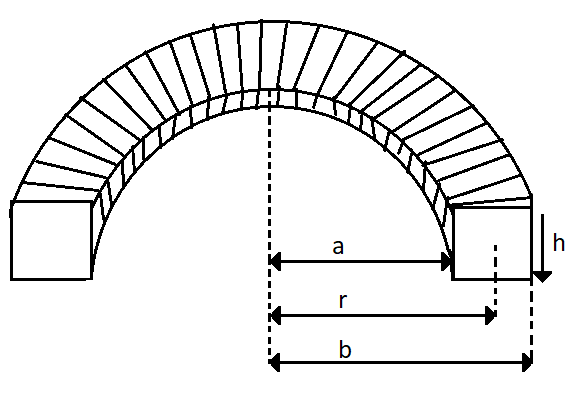
Now, let us consider a small section of height $ h $ and width $ dr $ .
Now, while applying the law,
 $\Rightarrow B \times 2\pi r = N{\mu _0}i $
To get the magnetic field strength, we can rearrange the equation as,
 $ \Rightarrow B = \dfrac{{N{\mu _0}i}}{{2\pi r}} $ …. Eq. (1)
The magnetic flux through this small section is given by the formula,
 $\Rightarrow d\phi = BdA $
So, the magnetic flux per turn is given by,
 $\Rightarrow \phi = \int {d\phi } = \int {BdA} $
The magnetic field is constant so it comes out of the integration as,
 $\Rightarrow \phi = B\int {dA} $
By substituting from eq. (1) we get,
 $\Rightarrow \phi = \dfrac{{N{\mu _0}ih}}{{2\pi }}\int_a^b {\dfrac{{dr}}{r}} $
Now, when integrating $ dr $ we set the limits from $ a $ to $ b $ . So on integrating we get,
 $\Rightarrow \phi = \dfrac{{N{\mu _0}ih}}{{2\pi }}\left[ {\ln r} \right]_a^b $
By substituting the variables,
$ \phi = \dfrac{{N{\mu _0}ih}}{{2\pi }}\left[ {\ln b - \ln a} \right] $
Hence, we get the flux as,
$ \phi = \dfrac{{{\mu _0}{N_i}h}}{{2\pi }}{\log _e}\dfrac{b}{a} $
Thus, the correct answer is option C.

Note
The Ampere’s circuital law is used to describe the relationship current and the magnetic field that is created by that current. This law can be written in its integral or differential form but ultimately all these forms are equivalent.