Question

The magnetic field $dB$ at a point r meter always from the current element $Id\vec l$aligned at angle of the $\theta $with respect to the current element is-
A) $\left( {\dfrac{{{\mu _0}}}{{4\pi }}} \right)\left( {\dfrac{{Id\vec l\sin \theta }}{r}} \right)$
B) $\left( {\dfrac{{{\mu _0}}}{{4\pi }}} \right)\left( {\dfrac{{Id\vec l}}{{{r^2}}}} \right)$
C) $\left( {\dfrac{{{\mu _0}}}{{4\pi }}} \right)\left( {\dfrac{{Id\vec l\sin \theta }}{{{r^2}}}} \right)$
D) $\left( {\dfrac{{{\mu _0}}}{{4\pi }}} \right)\left( {\dfrac{{Id\vec l}}{{{r^{}}}}} \right)$

Answer 1

Hint
It can be answered with the help of the Biot savart law, because this law gives the value of the $dB$ with the current element $Id\vec l$.

Complete answer:
According to the biot savart law-

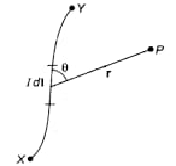
The magnetic field due the small length $dl$in which the I current flowing the conductor
Then
$dB \propto I$(current flowing in the conductor)
$dB \propto dl$ (small length)
$dB \propto \dfrac{1}{{{r^2}}}$ (inverse of the square of the distance of point p from the$dl$)
And $dB$α $\sin \theta $ (sine of the angle made by the $dl$ with point p)
Hence we can say that
$dB \propto \dfrac{{Id\vec l\sin \theta }}{{{r^2}}}$
Or it can be also written as
$dB$ = $K\dfrac{{Id\vec l\sin \theta }}{{{r^2}}}$
Where proportionality constant is equal to the $\dfrac{{{\mu _0}}}{{4\pi }}$
Or numerically it can be written as
$K = \dfrac{{{\mu _0}}}{{4\pi }}$
Hence the biot savart law
$dB$ = $\left( {\dfrac{{{\mu _0}}}{{4\pi }}} \right)\left( {\dfrac{{Id\vec l\sin \theta }}{{{r^2}}}} \right)$
The final answer is given by
$dB$ = $\left( {\dfrac{{{\mu _0}}}{{4\pi }}} \right)\left( {\dfrac{{Id\vec l\sin \theta }}{{{r^2}}}} \right)$.
Option (C) is the correct answer.

Note
This law was given by the two scientist biot and savart, they both were two different scientists who gave the value of the $dB$. The magnetic concept was firstly realized by the Oesterd's; he noticed that the needle of the magnet moved when current was passing from the wire nearer to it. He gave certain ways to find the direction of the magnetic field like a swimmer's rule.