Question

The magnetic field at the centre of an equilateral triangular loop of side 2L and carrying a current i is:
\[\begin{align}
  & A.\,\,\dfrac{9{{\mu }_{0}}i}{4\pi L} \\
 & B.\,\,\dfrac{3\sqrt{3}{{\mu }_{0}}i}{4\pi L} \\
 & C.\,\,\dfrac{2\sqrt{3}{{\mu }_{0}}i}{\pi L} \\
 & D.\,\,\dfrac{3{{\mu }_{0}}i}{4\pi L} \\
\end{align}\]

Answer 1

Hint: This is a question based on the concept of the magnetic field. The formula for computing the value of the magnetic field at the centre of the circular loop should be used, only the change being, the number of sides of a polygon should be multiplied to it.
Formula used:
\[B=\dfrac{{{\mu }_{0}}i\phi }{4\pi R}\]

Complete answer:
From the given information, we have the data as follows.
The side of an equilateral triangle is, 2L.
The magnetic field generated by a circular shape is,
\[B=\dfrac{{{\mu }_{0}}i\phi }{4\pi R}\]
Where i is current, R is the radius of the circular shape and is the angle (phase difference).
The magnetic field at the centre of an equilateral triangular loop carrying a current i is,
\[B=\dfrac{{{\mu }_{0}}i}{4\pi R}(\sin {{\theta }_{1}}+\sin {{\theta }_{2}})\times n\]
Here the value of n equals 3, as, the equilateral triangular loop is 3.
\[B=3\dfrac{{{\mu }_{0}}i}{4\pi R}(\sin {{\theta }_{1}}+\sin {{\theta }_{2}})\]

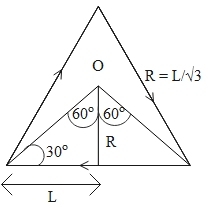
The value of R is \[R=\dfrac{L}{\sqrt{3}}\].
The values of the angles are, \[60{}^\circ \].
Substitute these values in the formula of the magnetic field at the centre of an equilateral triangular loop carrying a current i.
\[B=3\dfrac{{{\mu }_{0}}i}{4\pi \left( {}^{L}/{}_{\sqrt{3}} \right)}(\sin 60{}^\circ +\sin 60{}^\circ )\]
Continue further computation.
\[\begin{align}
  & B=3\dfrac{\sqrt{3}{{\mu }_{0}}i}{4\pi L}\left( \dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{3}}{2} \right) \\
 & \Rightarrow B=\dfrac{3\sqrt{3}{{\mu }_{0}}i}{4\pi L}\times \dfrac{2\sqrt{3}}{2} \\
 & \Rightarrow B=\dfrac{3\sqrt{3}{{\mu }_{0}}i}{4\pi L}\times \sqrt{3} \\
\end{align}\]
Thus, the value of the magnetic field at the centre of an equilateral triangular loop is \[B=\dfrac{9{{\mu }_{0}}i}{4\pi L}\], here i is the current flowing and L is half the length of the side of the triangle.
\[\therefore \] The magnetic field at the centre of an equilateral triangular loop of side 2L and carrying a current i is: \[\,\dfrac{9{{\mu }_{0}}i}{4\pi L}\].

Thus, option (A) is correct.

Note:
The angle or the phase difference must be expressed in radians. In this question the magnetic field at the centre of an equilateral triangular loop is asked, so, we have multiplied the number of sides of a triangle, that is, 3 to the magnetic field formula. Similarly, if the magnetic field is asked for a square, then we have to multiply the magnetic field by 4.