Question

The locus of the midpoints of chords of the circle \[{x^2} + {y^2} = 1\]which subtends a right angle at the origin is

A.\[{x^2} + {y^2} = \dfrac{1}{4}\]
B.\[{x^2} + {y^2} = \dfrac{1}{2}\]
C.\[xy = 0\]
D.\[{x^2} - {y^2} = 0\]

Answer 1

Hint: In this question equation of the circle is given, and the coordinate of center and vertex is also given, so we will find the radius of the circle by comparing it with the length of the cord, and then the chord equation is found.

Complete step-by-step answer:
Given the center of the circle, C is at \[(0,0)\]
R is the radius of the circle
Equation of the circle \[{x^2} + {y^2} = 1\]

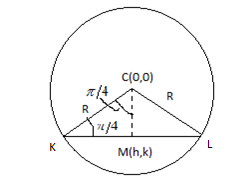
In the figure, we can see line CM is perpendicular to the KL; hence we apply the right-angled property in\[\Delta CKM\]; therefore, the length of line CM will be
\[CM = R\sin \dfrac{\pi }{4} = \dfrac{R}{{\sqrt 2 }} - - (i)\] [Since\[\sin \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }}\]]
By squaring both sides of the equation (i), we can further write
\[
  {\left( {CM} \right)^2} = {\left( {\dfrac{R}{{\sqrt 2 }}} \right)^2} \\
  {\Rightarrow \left( {CM} \right)^2} = \dfrac{{{R^2}}}{2} - - (ii) \\
 \]
Now apply the distance formula in the line CM whose vertices are given as (0, 0) and (h, k), respectively
\[
  {\left( {CM} \right)^2} = {\left( {h - 0} \right)^2} + {\left( {k - 0} \right)^2} \\
\Rightarrow { \left( {CM} \right)^2} = {h^2} + {k^2} - - (iii) \\
 \]
Where \[{\left( {CM} \right)^2} = \dfrac{{{R^2}}}{2}\] from equation (ii)
Hence by comparing equation (ii) and (iii), we can write
\[{h^2} + {k^2} = \dfrac{{{R^2}}}{2} - - (iv)\]
Since the equation of the circle is given hence by replacing h, k by x, y and radius R with 1 in equation (iv), we get the equation as
\[
  {x^2} + {y^2} = \dfrac{{{1^2}}}{2} \\
\Rightarrow {x^2} + {y^2} = \dfrac{1}{2} \\
 \]
Hence the locus of the midpoints \[{x^2} + {y^2} = \dfrac{1}{2}\]
Option (B) is correct.

Note: A chord of a circle is the straight line drawn between the ends point of the circle, where the diameter is the longest chord passing through the center, joining both endpoints at the circumference.