Question

The locus of the mid-point of those chord of the circle ${{x}^{2}}+{{y}^{2}}=4$ which subtend a right angle at the origin is –

(a) ${{x}^{2}}+{{y}^{2}}-2x-2y=0$
(b) ${{x}^{2}}+{{y}^{2}}=4$
(c) ${{x}^{2}}+{{y}^{2}}=2$
(d) \[{{\left( x-1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=5\]

Answer 1

Hint: This question is based on concept of locus and property of chord of circle. First of all, we assume the coordinate of the midpoint of the chord is$\left( h,k \right)$. Let the chord is $AB$ and the parametric points $A$ and $B$ are $\left( 2\cos \theta ,2\sin \theta \right)$ and $\left( 2\sin \varphi ,2\cos \varphi \right)$ respectively. Now using mid-point theorem and perpendicular formula, we solve for locus of$\left( h,k \right)$. By solving equation, we eliminate parametric variables and at last replace $h$ with $x$ and $k$ with$y$.
(i) Mid-point Theorem: If $M$ is midpoint of line segment$AB$, where $A$ is $\left( {{x}_{1}},{{y}_{1}} \right)$ and $B$ is $\left( {{x}_{2}},{{y}_{2}} \right)$, and let $M$ be $\left( x,y \right)$. Then
$x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}$ and $y=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}$.
(ii) Perpendicular formula: If two lines of slope ${{m}_{1}}$ and ${{m}_{2}}$ are perpendicular to each other, then
${{m}_{1}}\times {{m}_{2}}=-1$

Complete step-by-step answer:
Now, getting started with the solution, let’s write the given data.
Given equation of circle is ${{x}^{2}}+{{y}^{2}}=4$ … (i)
Centre is $\left( 0,0 \right)$ and radius $=2$
So, the circle can be represented as –

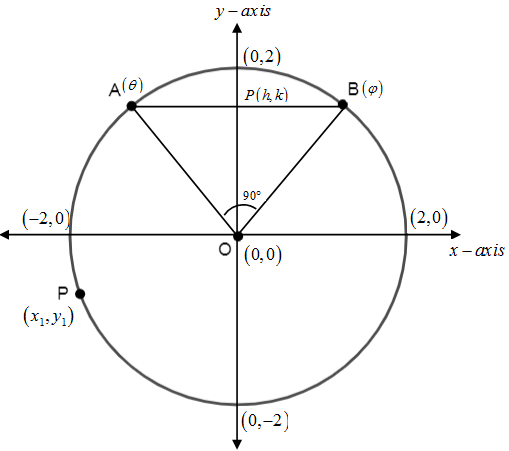
Let $AB$ is the chord of a circle joining parametric points $A\left( \theta \right)$ and$B\left( \varphi \right)$. So, $A$ is $\left( 2\cos \theta ,2\sin \theta \right)$ and $B$ is$\left( 2\cos \varphi ,2\sin \varphi \right)$.
As we know that, slope of line joining two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ $=\dfrac{\left( {{y}_{2}}-{{y}_{1}} \right)}{\left( {{x}_{2}}-{{x}_{1}} \right)}$.
So, slope of line $OA$ joining points $O\left( 0,0 \right)$ and $A\left( 2\cos \theta ,2\sin \theta \right)$ \[=\dfrac{\left( 2\sin \theta -0 \right)}{\left( 2\cos \theta -0 \right)}\]
$\Rightarrow {{m}_{OA}}=\tan \theta $
And, slope of line $OB$ joining $O\left( 0,0 \right)$ and $B\left( 2\cos \varphi ,2\sin \varphi \right)$ $==\dfrac{\left( 2\sin \varphi -0 \right)}{\left( 2\cos \varphi -0 \right)}$
$\Rightarrow {{m}_{OB}}=\tan \varphi $
Now, as we know that multiplication of two perpendicular lines of slope ${{m}_{1}}$ and ${{m}_{2}}$ is $\left( -1 \right)$.
${{m}_{1}}\times {{m}_{2}}=-1$
According to the question, $OA$ and $OB$ are perpendicular.
${{m}_{OA}}\times {{m}_{OB}}=-1$
$\Rightarrow \tan \theta \times \tan \varphi =-1$
\[\Rightarrow \dfrac{\sin \theta \times \sin \varphi }{\cos \theta \times \cos \varphi }=-1\]
\[\Rightarrow \cos \theta .\cos \varphi +\sin \theta .\sin \varphi =0\] … (ii)
Now as we know that midpoint $M\left( x,y \right)$ of line segment$AB$, where $A\left( {{x}_{1}},{{y}_{1}} \right)$ and $B\left( {{x}_{2}},{{y}_{2}} \right)$ is –
$x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}$ and$y=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}$.
Now let us assume midpoint of chord$AB$, where $A$ is $\left( 2\cos \theta ,2\sin \theta \right)$ and $B$ is $\left( 2\cos \varphi ,2\sin \varphi \right)$ is $P\left( h,k \right)$.
Then,
$h=\dfrac{2\cos \theta +2\cos \varphi }{2}$
$\Rightarrow h=\cos \theta +\cos \varphi $ … (iii)
$k=\dfrac{2\sin \theta +2\sin \varphi }{2}$
$\Rightarrow k=\sin \theta +\sin \varphi $ … (iv)
Now by adding squares of equation (iii) and (iv), we get
${{h}^{2}}={{\left( \cos \theta +\cos \varphi \right)}^{2}}$ and ${{k}^{2}}={{\left( \sin \theta +\sin \varphi \right)}^{2}}$
\[\Rightarrow {{h}^{2}}+{{k}^{2}}={{\cos }^{2}}\theta +{{\cos }^{2}}\varphi +2\cos \theta \cos \varphi +{{\sin }^{2}}\theta +{{\sin }^{2}}\varphi +2\sin \theta \sin \varphi \]
\[\because {{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1\]
\[\Rightarrow {{h}^{2}}+{{k}^{2}}=1+1+2\left( \cos \theta \cos \varphi +\sin \theta \sin \varphi \right)\]
Now by equation (ii), \[\cos \theta .\cos \varphi +\sin \theta .\sin \varphi =0\]
\[\Rightarrow {{h}^{2}}+{{k}^{2}}=2+0\]
\[\Rightarrow {{h}^{2}}+{{k}^{2}}=2\]
Now by replacing $h\to x$ and$k\to y$, we have
\[\Rightarrow {{x}^{2}}+{{y}^{2}}=2\]

So, the locus of the midpoint of chord is a circle, \[{{x}^{2}}+{{y}^{2}}=2\].

So, the correct answer is “Option A”.

Note: (i) In this type of question while solving equations, we should try to eliminate all other variables except $h$ and$k$, and get equations in $h$ and $k$.

(ii) In this question, we get an equation$\tan \theta \times \tan \varphi =-1$.
If we consider formula:
$\tan \left( \theta -\varphi \right)=\dfrac{\tan \theta -\tan \varphi }{1+\tan \theta .\tan \varphi }$
$\because \tan \left( \theta -\varphi \right)\to \infty $
$\Rightarrow \left( \theta -\varphi \right)=90{}^\circ $
$\Rightarrow \theta =90{}^\circ +\varphi $
We can use this relation also to solve the equation at last.

(iii) Here, students should take care while squaring and adding the two equations that there should not be any calculation mistakes, otherwise the whole question will be wrong.