Question

The locus of the midpoint of the chord of the circle ${{x}^{2}}+{{y}^{2}}-2x-2y-2=0$ which makes an angle of $120{}^\circ $ at the centre is –
(a) ${{x}^{2}}+{{y}^{2}}-2x-2y+1=0$
(b) ${{x}^{2}}+{{y}^{2}}+x+y-1=0$
(c) ${{x}^{2}}+{{y}^{2}}-2x-2y-1=0$
(d) None of these

Answer 1

Hint: This question involves mid-point theorem, parametric points of circle and concept of locus. First of all, we assume a chord in the form of parametric points and then by mid-point theorem, get the midpoint of the chord. Let us assume mid-point as and solve for the equation in terms of $h$ and $k$ and then replace $h$ with $x$ and $k$ with$y$.
We will use following properties and formula –
(i) If $\alpha $ is the angle between two lines of slope ${{m}_{1}}$ and${{m}_{2}}$, then
$\tan \alpha =\dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}}$
(ii) Mid-point Theorem: If $M$ is midpoint of line segment$AB$, where $A$ is $\left( {{x}_{1}},{{y}_{1}} \right)$ and $B$ is$\left( {{x}_{2}},{{y}_{2}} \right)$, and let $M$ be $\left( x,y \right)$. Then
$x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}$ and$y=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}$.

Complete step-by-step answer:
Now, we have been given that the equation of circle is ${{x}^{2}}+{{y}^{2}}-2x-2y-2=0$
$\Rightarrow \left( {{x}^{2}}-2x+1 \right)+\left( {{y}^{2}}-2y+1 \right)-2-2=0$
$\Rightarrow {{\left( x-1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=4$ … (i)
$\Rightarrow {{\left( x-1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}={{2}^{2}}$
So, the centre is $\left( 1,1 \right)$ and radius is $2$.
Thus, the circle can be represented as –

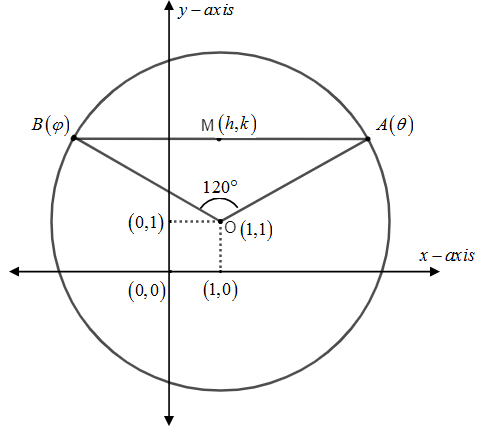
As we know that if the equation of a circle is${{\left( x-\alpha \right)}^{2}}+{{\left( y-\beta \right)}^{2}}={{r}^{2}}$, then parametric point $P$ is assumed as $P\left( \theta \right)$.
${{x}_{1}}=\left( \alpha +r\cos \theta \right)$ and${{y}_{1}}=\left( \beta +r\sin \theta \right)$
Let us assume $AB$in the parametric form of points $A\left( \theta \right)$ and$B\left( \varphi \right)$. So, $A$ is $\left( 1+2\cos \theta ,1+2\sin \theta \right)$ and $B$ is$\left( 1+2\cos \varphi ,1+2\sin \varphi \right)$.
As we know that, slope of line joining two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and$\left( {{x}_{2}},{{y}_{2}} \right)$ $=\dfrac{\left( {{y}_{2}}-{{y}_{1}} \right)}{\left( {{x}_{2}}-{{x}_{1}} \right)}$.
So, slope of line $OA$ joining points $O\left( 0,0 \right)$ and $A\left( 1+2\cos \theta ,1+2\sin \theta \right)$ \[=\dfrac{\left( 1+2\sin \theta \right)-1}{\left( 1+2\cos \theta \right)-1}\]
$\Rightarrow {{m}_{OA}}=\tan \theta $
And, slope of line $OB$ joining $O\left( 0,0 \right)$ and $B\left( 1+2\cos \varphi ,1+2\sin \varphi \right)$ $=\dfrac{\left( 1+2\sin \varphi \right)-1}{\left( 1+2\cos \varphi \right)-1}$
$\Rightarrow {{m}_{OB}}=\tan \varphi $
As we know that, if $\alpha $ is the angle between two lines of slope ${{m}_{1}}$ and${{m}_{2}}$, then
$\tan \alpha =\dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}}$ .
Now according to the question, angle between line $OA$ and $OB$ is
$\tan \left( 120{}^\circ \right)=\dfrac{{{m}_{OA}}-{{m}_{OB}}}{1+{{m}_{OA}}.{{m}_{OB}}}$
$\Rightarrow \tan \left( 120{}^\circ \right)=\dfrac{\tan \theta -\tan \varphi }{1+\tan \theta .\tan \varphi }$
$\Rightarrow \tan \left( 120{}^\circ \right)=\tan \left( \theta -\varphi \right)$
$\Rightarrow 120{}^\circ =\left( \theta -\varphi \right)$ … (iii)
Now, as we know that, if $M\left( x,y \right)$ is midpoint of line segment$AB$, where $A$ is $\left( {{x}_{1}},{{y}_{1}} \right)$ and $B$ is$\left( {{x}_{2}},{{y}_{2}} \right)$, then
$x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}$ and$y=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}$.
Let midpoint of the chord $AB$ is $M\left( h,k \right)$ and $A$ is $\left( 1+2\cos \theta ,1+2\sin \theta \right)$ and $B$ is$\left( 1+2\cos \varphi ,1+2\sin \varphi \right)$.
$h=\dfrac{\left( 1+2\cos \theta \right)+\left( 1+2\cos \varphi \right)}{2}$
\[\Rightarrow 2h=2+2\left( \cos \theta +\cos \varphi \right)\]
\[\Rightarrow h-1=\cos \theta +\cos \varphi \]
\[\Rightarrow {{\left( h-1 \right)}^{2}}={{\left( \cos \theta +\cos \varphi \right)}^{2}}\] … (iii)
And, $k=\dfrac{\left( 1+2\sin \theta \right)+\left( 1+2\sin \varphi \right)}{2}$
\[\Rightarrow 2k=2+2\left( \sin \theta +\sin \varphi \right)\]
\[\Rightarrow k-1=\sin \theta +\sin \varphi \]
\[\Rightarrow {{\left( k-1 \right)}^{2}}={{\left( \sin \theta +\sin \varphi \right)}^{2}}\] … (iv)
By adding equation (iii) and (iv), we get
\[\Rightarrow {{\left( h-1 \right)}^{2}}+{{\left( k-1 \right)}^{2}}={{\cos }^{2}}\theta +{{\cos }^{2}}\varphi +2\cos \theta \cos \varphi +{{\sin }^{2}}\theta +{{\sin }^{2}}\varphi +2\sin \theta \sin \varphi \]
\[\because {{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1\] and $\cos {{\theta }_{1}}.\cos {{\theta }_{2}}+\sin {{\theta }_{1}}.\sin {{\theta }_{2}}=\cos \left( {{\theta }_{1}}-{{\theta }_{2}} \right)$
\[\Rightarrow {{\left( h-1 \right)}^{2}}+{{\left( k-1 \right)}^{2}}=2+2\cos \left( \theta -\varphi \right)\]
As we know from equation (iii), $\left( \theta -\varphi \right)=120{}^\circ $ , so we have
\[\Rightarrow {{\left( h-1 \right)}^{2}}+{{\left( k-1 \right)}^{2}}=2+2\cos \left( 120{}^\circ \right)\]
\[\Rightarrow {{\left( h-1 \right)}^{2}}+{{\left( k-1 \right)}^{2}}=2+2\left( \dfrac{-1}{2} \right)\]
\[\Rightarrow {{\left( h-1 \right)}^{2}}+{{\left( k-1 \right)}^{2}}=1\]
Now by replacing $h\to x$ and$k\to y$, we have
\[\Rightarrow {{\left( x-1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=1\]
\[\Rightarrow {{x}^{2}}-2x+1+{{y}^{2}}-2y+1=1\]
\[\Rightarrow {{x}^{2}}+{{y}^{2}}-2x-2y+1=0\]

 So, the locus of the midpoint of the chord is \[{{x}^{2}}+{{y}^{2}}-2x-2y+1=0\].

So, the correct answer is “Option A”.

Note: (i) In this question, students should take care of the angle between two lines formula,
$\tan \alpha =\dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}}$
Don’t interchange the two signs; else it will make the whole question wrong.

(ii) Students should take care of calculation mistakes. In options, there is only change in signs. So, take care of signs properly.