Question

The locus of point of trisections of the focal chords of the parabola, ${y^2} = 4x$:
A.${y^2} = x - 1$
B.$9{y^2} = 4\left( {3x - 4} \right)$
C.\[{y^2} = 2\left( {1 - x} \right)\]
D.None of these

Answer 1

Hint: Draw the diagram according to the question. Construct a double ordinate passing through the focus. Express the point of trisection in terms of the parametric equation of the parabola. Substitute the values of parametric in the equation of the parabola to find the locus.

Complete step-by-step answer:
Draw a figure corresponding to the given conditions.

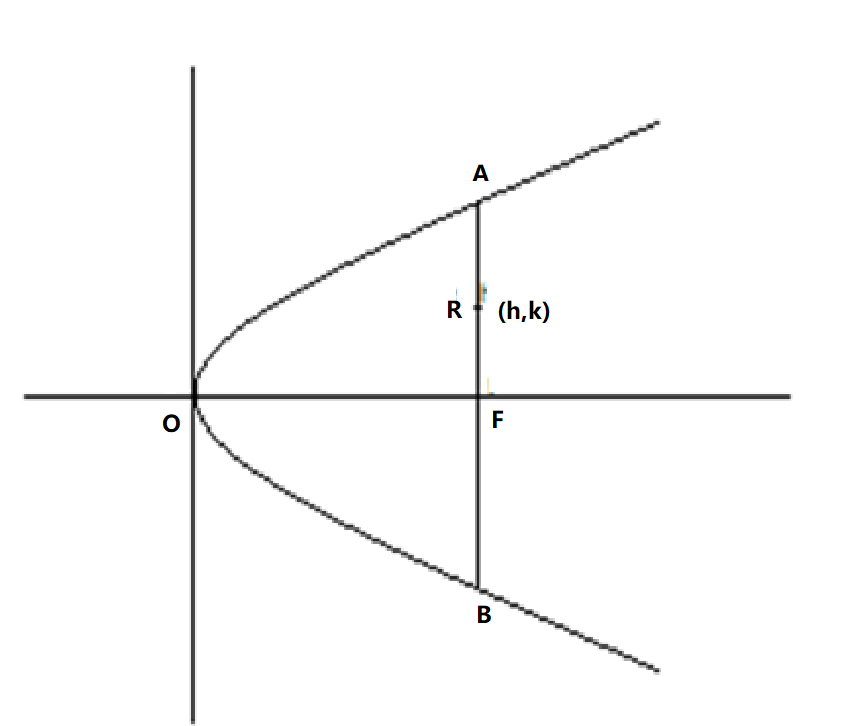
Let $F$be the focus of the parabola and let$AB$ be the ordinate passing through the focus of the parabola.
Also, let the focal ordinate is trisected by the point $B$.
Let the coordinates of the point $B$ be represented by $\left( {h,k} \right)$.
Write the parametric coordinates of the point such that lie on the parabola.
A point on the parabola can also be represented as $\left( {{t^2},2t} \right)$.
Now, we want to find the points that trisects the focal chord.

Therefore, the point $A$is written as $\left( {{t^2},2t} \right)$, and the point $B$ is $\left( {{t^2}, - 2t} \right)$ .
Since, \[B\] trisect the line of the double ordinate , so, point \[B\] divides the line $AB$ in the ratio 1:2
The $y$ coordinate of the point $B$ can be found using the section formula \[\dfrac{{m\left( {{y_1}} \right) + n\left( {{y_2}} \right)}}{{m + n}}\].
Here $m = 1,n = 2,{y_1} = - 2t,{y_2} = 2t$
$
  k = \dfrac{{2\left( {2t} \right) - 1\left( {2t} \right)}}{3} \\
  3k = 2t \\
$
The $x$coordinate of the point $B$is $h = {t^2}$
Thus, $\left( {{t^2},2t} \right)$ is equivalent to $\left( {h,3k} \right)$
Since the points $\left( {{t^2},2t} \right)$ represent the parametric equation of the parabola ${y^2} = 4x$, they should satisfy the equation.
$
  {y^2} = 4x \\
  {\left( {3k} \right)^2} = 4h \\
  9{k^2} = 4h \\
 $
Replacing the coordinate $\left( {h,k} \right)$ with $\left( {x,y} \right)$,we get the equation for the locus of the trisection of the focal chord of the parabola ${y^2} = 4x$.
$9{y^2} = 4x$
Thus the option D None of these is the correct answer.
Note: The parametric coordinates for the parabola ${y^2} = 4ax$ is $\left( {a{t^2},2at} \right)$. The focus of the parabola is located at the point \[\left( {a,0} \right)\]. The focal chord passing that is perpendicular to the horizontal axis for the parabola ${y^2} = 4ax$ is called the double ordinate.