Question

The locus of point of intersection of the lines, \[\sqrt{2}x-y+4\sqrt{2}k=0\] and \[\sqrt{2}kx+ky-4\sqrt{2}=0\] (k is any non-zero real parameter), is?
\[\begin{align}
  & (A)\text{ A hyperbola with length of its transverse axis is 8}\sqrt{2}. \\
 & (B)\text{ An ellipse with length of its major axis is 8}\sqrt{2}. \\
 & (C)\text{ An ellipse whose eccentricity is }\dfrac{1}{\sqrt{3}}. \\
 & (D)\text{ A hyperbola whose eccentricity is }\sqrt{3.} \\
\end{align}\]

Answer 1

Hint: We need to solve the given lines and find the coordinates of intersection points of given lines. We should multiply the first equation by k and then we should add the first equation to the second equation. So that we can get the x in terms of k. Similarly, we can find y in terms of k. This will provide the abscissa and ordinate of intersection points. Now we needed to obtain the relation between the abscissa and ordinate of intersection point. This relation defines the locus of points of intersection of lines. After finding the equation of locus, it is required to find the nature of the equation of locus as well as the properties of locus.

Complete step-by-step answer:
From the question, it is clear that we needed to solve the line equation \[\sqrt{2}x-y+4\sqrt{2}k=0\] and \[\sqrt{2}kx+ky-4\sqrt{2}=0\] where k is any non-zero parameter.
Consider
\[\sqrt{2}x-y+4\sqrt{2}k=0.......(1)\]
\[\sqrt{2}kx+ky-4\sqrt{2}=0.......(2)\]
Let us multiply equation (1) with “k” on both sides.
\[\sqrt{2}kx-ky+4\sqrt{2}{{k}^{2}}=0......(3)\]

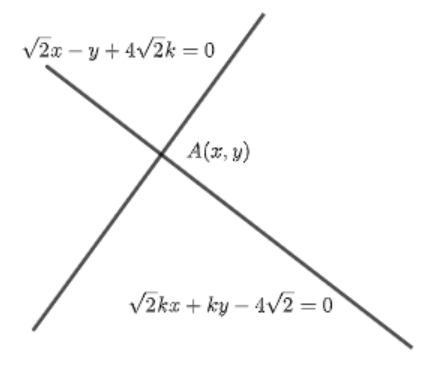
Let us assume an intersection point of \[\sqrt{2}x-y+4\sqrt{2}k=0\] and \[\sqrt{2}kx+ky-4\sqrt{2}=0\] as \[A\left( x,y \right)\].
We needed to add equation (2) and equation (3) to find the x-coordinate of A.
\[\left( \sqrt{2}kx+ky-4\sqrt{2} \right)+\left( \sqrt{2}kx-ky+4\sqrt{2}{{k}^{2}} \right)=0\]
\[\Rightarrow 2\sqrt{2}kx-4\sqrt{2}+4\sqrt{2}{{k}^{2}}=0\]
\[\Rightarrow 2\sqrt{2}kx=4\sqrt{2}-4\sqrt{2}{{k}^{2}}\]
\[\Rightarrow 2\sqrt{2}kx=4\sqrt{2}\left( 1-{{k}^{2}} \right)........(4)\]
Now, we should divide equation (4) with \[2\sqrt{2}\]
\[\Rightarrow \dfrac{2\sqrt{2}kx}{2\sqrt{2}}=\dfrac{4\sqrt{2}}{2\sqrt{2}}\left( 1-{{k}^{2}} \right)\]
\[\Rightarrow kx=2\left( 1-{{k}^{2}} \right)\]
\[\Rightarrow x=\dfrac{2\left( 1-{{k}^{2}} \right)}{k}......(5)\]
Substitute equation (5) equation (1) to obtain the y-coordinate of A.
\[\Rightarrow \sqrt{2}k\left( \dfrac{2(1-{{k}^{2}})}{k} \right)+ky-4\sqrt{2}=0\]
\[\Rightarrow 2\sqrt{2}\left( 1-{{k}^{2}} \right)+ky-4\sqrt{2}=0\]
\[\Rightarrow ky=4\sqrt{2}-2\sqrt{2}(1-{{k}^{2}})\]
\[\Rightarrow ky=2\sqrt{2}\left( 1+{{k}^{2}} \right)\]
\[\Rightarrow y=\dfrac{2\sqrt{2}(1+{{k}^{2}})}{k}......(6)\]
Hence, the point A is \[A\left( \dfrac{2\left( 1-{{k}^{2}} \right)}{k},\dfrac{2\sqrt{2}(1+{{k}^{2}})}{k} \right)\].
From equation (5),
\[\Rightarrow x=\dfrac{2\left( 1-{{k}^{2}} \right)}{k}\]
Now divide the equation by 2 on both sides.
\[\Rightarrow \dfrac{x}{2}=\dfrac{\left( 1-{{k}^{2}} \right)}{k}.......(7)\]
Now squaring the equation (7) on both sides.
\[\Rightarrow {{\left( \dfrac{x}{2} \right)}^{2}}={{\left( \dfrac{\left( 1-{{k}^{2}} \right)}{k} \right)}^{2}}\]
\[\Rightarrow \dfrac{{{x}^{2}}}{4}=\dfrac{{{\left( 1-{{k}^{2}} \right)}^{2}}}{{{k}^{2}}}........(8)\]
From equation (6),
\[\Rightarrow y=\dfrac{2\sqrt{2}(1+{{k}^{2}})}{k}\]
Now divide the equation by \[2\sqrt{2}\] on both sides.
\[\Rightarrow \dfrac{y}{2\sqrt{2}}=\dfrac{\left( 1+{{k}^{2}} \right)}{k}.......(9)\]
Now squaring the equation (9) on both sides.
\[\Rightarrow {{\left( \dfrac{y}{2\sqrt{2}} \right)}^{2}}={{\left( \dfrac{1+{{k}^{2}}}{k} \right)}^{2}}\]
\[\Rightarrow \dfrac{{{y}^{2}}}{8}=\dfrac{{{\left( 1+{{k}^{2}} \right)}^{2}}}{{{k}^{2}}}.......(10)\]
Now we should subtract equation (8) and equation (10).
\[\Rightarrow \dfrac{{{x}^{2}}}{4}-\dfrac{{{y}^{2}}}{8}=\dfrac{{{\left( 1-{{k}^{2}} \right)}^{2}}}{{{k}^{2}}}-\dfrac{{{\left( 1+{{k}^{2}} \right)}^{2}}}{{{k}^{2}}}\]
\[\Rightarrow \dfrac{{{x}^{2}}}{4}-\dfrac{{{y}^{2}}}{8}=\dfrac{{{\left( 1-{{k}^{2}} \right)}^{2}}-{{\left( 1+{{k}^{2}} \right)}^{2}}}{{{k}^{2}}}\]
\[\Rightarrow \dfrac{{{x}^{2}}}{4}-\dfrac{{{y}^{2}}}{8}=\dfrac{\left( 1+{{k}^{4}}-2{{k}^{2}} \right)-\left( 1+{{k}^{4}}+2{{k}^{2}} \right)}{{{k}^{2}}}\]
\[\Rightarrow \dfrac{{{x}^{2}}}{4}-\dfrac{{{y}^{2}}}{8}=\dfrac{1+{{k}^{4}}-2{{k}^{2}}-1-{{k}^{4}}-2{{k}^{2}}}{{{k}^{2}}}\]
\[\Rightarrow \dfrac{{{x}^{2}}}{4}-\dfrac{{{y}^{2}}}{8}=\dfrac{-4{{k}^{2}}}{{{k}^{2}}}\]
\[\begin{align}
  & \Rightarrow \dfrac{{{x}^{2}}}{4}-\dfrac{{{y}^{2}}}{8}=-4......(11) \\
 & \\
\end{align}\]
Now we should divide equation (11) with 4 on both sides.
\[\Rightarrow \dfrac{{{x}^{2}}}{16}-\dfrac{{{y}^{2}}}{32}=-1......(12)\]

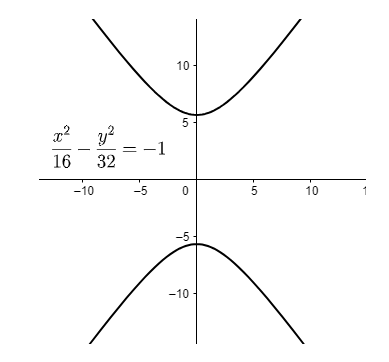
We know that the equations like \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=\pm 1\]represents hyperbola. Hence, we can say that the equation (12) is a hyperbola.
From equation (12),
\[{{a}^{2}}=16\]
Apply square root on both sides,
\[a=4.....(13)\].
From equation (12),
\[{{b}^{2}}=32\]
Apply square root on both sides,
\[b=\sqrt{32}\]
\[\Rightarrow b=4\sqrt{2}......(14)\]
For a hyperbola \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=-1\], the length of transverse axis is 2b and the length of conjugate axis is 2a.
Hence, Length of transverse axis of \[\dfrac{{{x}^{2}}}{16}-\dfrac{{{y}^{2}}}{32}=-1\] is \[2b=2(4\sqrt{2})=8\sqrt{2}\].
We know that the eccentricity of hyperbola \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=-1\] is \[e=\sqrt{1+\dfrac{{{a}^{2}}}{{{b}^{2}}}}\].
Hence, the eccentricity of hyperbola \[\dfrac{{{x}^{2}}}{16}-\dfrac{{{y}^{2}}}{32}=-1\]is \[e=\sqrt{1+\dfrac{16}{32}}=\sqrt{1+\dfrac{1}{2}}=\sqrt{\dfrac{3}{2}}\].
Therefore, option (A) is correct.

Note: Most of the students may go wrong by using the same formulae for both the hyperbolic equations \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=-1\] and \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\]. One must understand the difference between the formulae use for both the equations \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=-1\] and \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\].
The eccentricity of hyperbola \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=-1\] is \[e=\sqrt{1+\dfrac{{{a}^{2}}}{{{b}^{2}}}}\]. The length of transverse axis of \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=-1\] is 2b and the length of conjugate axis of \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=-1\] is 2a.
The eccentricity of hyperbola \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\] is \[e=\sqrt{1+\dfrac{{{b}^{2}}}{{{a}^{2}}}}\]. The length of transverse axis of \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\] is 2a and the length of conjugate axis of \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\] is 2b. We must be careful and we should use respective formulae for respective hyperbola.