Question

The locus of a point at the tip of a minute hand of a clock moving from \[3:15PM\] to \[3:45PM\] on a particular day is
A. A circle
B. A horizontal line
C. A quadrant
D. A semicircle

Answer 1

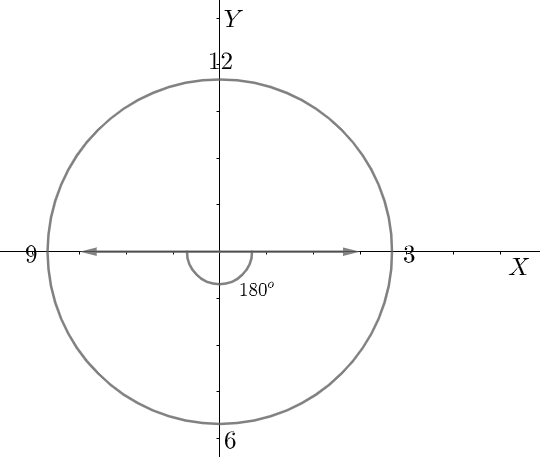
Hint: We first note what is the starting point and finishing point of the minute hand. Then, we compare the clock to Cartesian coordinate axes. The number $3$ on the clock shows the positive x axis, the number $9$ on the clock shows the negative x axis, the number $12$ on the clock shows the positive y axis and the number $6$ on the clock shows the negative y axis. As the minute hand moves from the positive x axis to the negative x axis, it completes a ${{180}^{\circ }}$ turn, which is half a complete turn, from which we get our final answer.

Complete step-by-step solution:
A locus is the path traversed by a point given that the point moves satisfying an underline equation or condition. It is the set of all the points that satisfy a given equation or condition. For example, the locus of a point such that the point is at a constant distance from a fixed point is a circle.
Now, if we compare a clock with Cartesian coordinate axes, then the number $3$ on the clock shows the positive x axis, the number $9$ on the clock shows the negative x axis, the number $12$ on the clock shows the positive y axis and the number $6$ on the clock shows the negative y axis. Now, since the length of the minute hand is constant, we can say that the locus of any particular point on it is a circular arc in general. As the minute hand moves from the positive x axis to the negative x axis, it completes a ${{180}^{\circ }}$ turn, which is half a complete turn, or half a circle.
Thus, we can conclude that the locus of a point at the tip of a minute hand of a clock moving from \[3:15PM\] to \[3:45PM\] on a particular day is a semicircle which is Option D.

Note: These problems are easy if we can visualize the clock completely. Students often mistakenly write the answer as a circle though they know that it is a semicircle. These mistakes should be avoided. Also, it's better if we draw a rough sketch of a clock and then solve it.