Question

The List-I below gives some quantities involved in a process and List-II gives some possible values of these quantities.

If the process carried out on one mole of monatomic ideal gas is as shown in figure in the PV-diagram with ${P_0}{V_0} = \dfrac{1}{3}R{T_0}$ the correct match is,

A. I → S, II → R, III → Q, IV → T
B. I → Q, II → R, III → P, IV → U
C. I → Q, II → S, III → R, IV → U
D. I → Q, II → R, III → S, IV → U

Answer 1

Hint: Ideal gas is a perfect gas in which there will be no interaction between the constituent molecules. One molecule will not be affected by the other molecule. These molecules occupy a negligible amount of space and they always obey gas laws. We solve this problem using the gas laws.

Formula used:
$\eqalign{
  & \Delta Q = \Delta U + \Delta W \cr
  & \Delta U = n{C_V}\Delta T \cr
  & \Delta W = P\Delta V \cr
  & {C_V} = \dfrac{f}{2}R \cr
  & \Delta PV = nR\Delta T \cr} $

Complete step by step answer:
By referring the diagram below we will try to answer the questions asked

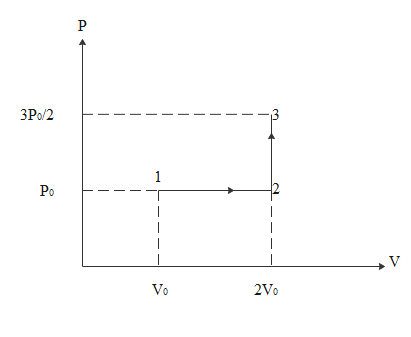
Work done in the process 1-2-3 will be equal to work done in 1-2 only. This is because the formula for work done is $\Delta W = P\Delta V$
In the process 2-3 changes in volume is zero. so work done will be zero
For the process 1-2 work done will be
$\Delta W = P\Delta V$
$\eqalign{
  & \Rightarrow \Delta W = P({V_2} - {V_1}) \cr
  & \Rightarrow \Delta W = {P_0}(2{V_0} - {V_0}) \cr
  & \Rightarrow \Delta W = {P_0}{V_0} \cr
  & \Rightarrow {P_0}{V_0} = \dfrac{1}{3}R{T_0} \cr
  & \therefore \Delta W = \dfrac{1}{3}R{T_0} \cr} $
Change in internal energy in process $1 \to 2 \to 3$ is $\Delta U = n{C_V}\Delta T$
The degrees of freedom(f) for monatomic gas is 3. Number of moles(n) is one.
For ideal gas $\Delta PV = nR\Delta T$
$\Delta U = n{C_V}\Delta T$
$\eqalign{
  & \Rightarrow \Delta U = n{C_V}\Delta T \cr
  & \Rightarrow \Delta U = n\left( {\dfrac{f}{2}R} \right)\Delta T \cr
  & \Rightarrow f = 3 \cr
  & \Rightarrow \Delta U = n\left( {\dfrac{3}{2}R} \right)\Delta T \cr
  & \Rightarrow \Delta U = \dfrac{3}{2}nR\Delta T \cr
  & \Rightarrow \Delta U = \dfrac{3}{2}(\Delta PV) \cr
  & \Rightarrow \Delta U = \dfrac{3}{2}({P_3}{V_3} - {P_1}{V_1}) \cr
  & \Rightarrow \Delta U = \dfrac{3}{2}(\dfrac{{3{P_0}}}{2}\left( {2{V_0}} \right) - {P_0}{V_0}) \cr
  & \Rightarrow \Delta U = 3{P_0}{V_0} \cr
  & \Rightarrow {P_0}{V_0} = \dfrac{1}{3}R{T_0} \cr
  & \therefore \Delta U = R{T_0} \cr} $
Heat absorbed by the system in process $1 \to 2 \to 3$ will be found out by using first law of thermodynamics $\Delta Q = \Delta U + \Delta W$
It states that the amount of heat given is used to do work on the system and to raise the internal energy of the system.
$\Delta Q = \Delta U + \Delta W$
$ \Rightarrow \Delta U = R{T_0}$
$ \Rightarrow \Delta W = \dfrac{1}{3}R{T_0}$
$\eqalign{
  & \Rightarrow \Delta Q = R{T_0} + \dfrac{1}{3}R{T_0} \cr
  & \therefore \Delta Q = \dfrac{4}{3}R{T_0} \cr} $
Heat absorbed by the system in process $1 \to 2$ will be found from same equation $\Delta Q = \Delta U + \Delta W$
$\Delta Q = \Delta U + \Delta W$
$\eqalign{
  & \Rightarrow \Delta U = \dfrac{3}{2}(\Delta PV) \cr
  & \Rightarrow \Delta Q = \dfrac{3}{2}(\Delta PV) + \Delta W \cr
  & \Rightarrow \Delta Q = \dfrac{3}{2}({P_0}2{V_0} - {P_0}{V_0}) + {P_0}{V_0} \cr
  & \Rightarrow \Delta Q = \dfrac{5}{2}{P_0}{V_0} \cr
  & \Rightarrow {P_0}{V_0} = \dfrac{1}{3}R{T_0} \cr
  & \Rightarrow \Delta Q = \dfrac{5}{2}\dfrac{{R{T_0}}}{3} \cr
  & \therefore \Delta Q = \dfrac{{5R{T_0}}}{6} \cr} $
Hence I → Q, II → R, III → S, IV → U is correct
So option D is correct.

Note:
All the ideal gas laws we apply are valid only for the ideal gases. At low temperatures and high pressures there will be interactions between the molecules of the gases. Hence they deviate from the ideal gas behaviour. Usually gases behave as ideal gases at higher temperatures and lower pressures.