Question

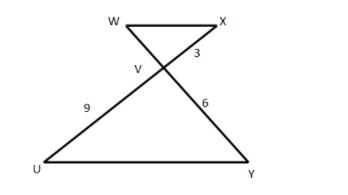
The lines \[UX\] and $WY$ intersects at point $V$ and $UY$ and $WX$ are parallel lines, then the length of $WY$ is:

A.8
B.9
C.10
D.12

Answer 1

Hint: Here, we are required to find the length of $WY$ when it intersects with the line \[UX\] at point $V$ such that $UY$ and $WX$ are parallel lines. We will use the properties of parallel lines intersected by a transversal to prove that the two triangles which are formed due to intersection of these lines are similar. Then by using CSST Rule, we will find the length of $VW$; which will ultimately help us to find the required length of $WY$.

Complete step-by-step answer:
According to the question,
We are given two lines \[UX\] and $WY$ which intersect each other at point $V$ such that:
$UY\parallel WX$ .
Now, since $UY\parallel WX$ and \[UX\] is the transversal
Therefore, $\angle U = \angle X$…………………………(1)
This is because, when two lines are parallel and a transversal passes through them, then the alternate angles are always equal.
Similarly, we can say that when $UY\parallel WX$ and $WY$ is the transversal,
Then, $\angle Y = \angle W$ (alternate angles) ……………………………..(2)
Therefore, from (1) and (2),
$\vartriangle VWX \sim \vartriangle VYU$ (By Angle-Angle or AA similarity)
Now, when two triangles are similar, then corresponding sides of those similar triangles are also similar to each other, this is also known as CSST Rule.
Therefore, we can say that when,
$\vartriangle VWX \sim \vartriangle VYU$
Then, $\dfrac{{VW}}{{VY}} = \dfrac{{WX}}{{YU}} = \dfrac{{VX}}{{VU}}$ (By CSST)……………………….(3)
According to the question,
$VX = 3$, $VY = 6$ and $VU = 9$
Hence, substituting these values in the first and the third fraction of (3), we get,
$\dfrac{{VW}}{6} = \dfrac{3}{9}$
$ \Rightarrow \dfrac{{VW}}{6} = \dfrac{1}{3}$
$ \Rightarrow VW = \dfrac{6}{3} = 2$
Hence, the value of $VW$ is 2 units.
Now, we have to find the length of $WY$.
Clearly, from the given figure,
$WY = VW + VY$
Substituting $VW = 2$ and $VY = 6$,
Hence, $WY = 2 + 6 = 8$
Hence, the required length of $WY$ is 8 units.
Therefore, option A is the correct answer.

Note: When we will prove the similarities of the two triangles, then, it is really important to apply the ‘CSST Rule’ carefully. According to this rule, the corresponding sides of similar triangles are similar to each other. This means that their fraction will be equal. Now, while writing the sides in fraction, we should keep in mind that if in the first fraction, we are taking the numerator as one of the sides of the first triangle then, in the second and third fractions, the numerators should be the sides of the first triangle itself. If we assume the numerators and denominators without keeping in mind the triangles and their respective sides, then after solving the fractions, we will get a wrong value as the number which should be divided would be multiplied and vice-versa.