Question

The line x+3y-2= 0 bisects the angle between a pair of lines one of which has the equation x-7y+5 =0. Find the equation of the other line.

Answer 1

Hint: Assume that the equation of the line is y = mx+c. Use the fact that the angle between two lines of slopes ${{m}_{1}}$ and ${{m}_{2}}$ is given by $\phi ={{\tan }^{-1}}\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right|$. Hence find the angle between the lines x+3y-2 = 0 and x-7y+5 = 0 and also the angle between the lines x+3y-2=0 and y = mx+c. Equate the two angles and hence form an equation in m. Solve for me and hence find the slope of the line. Use the fact that the pair of lines and the angle bisector of the pair are concurrent. Hence the line y = mx+c must pass through the point of intersection of x-7y+5 = 0 and x+3y-2 = 0. Hence find the value of c and hence find the equation of the line.

Complete step-by-step answer:
Let the equation of the line be y = mx+c.

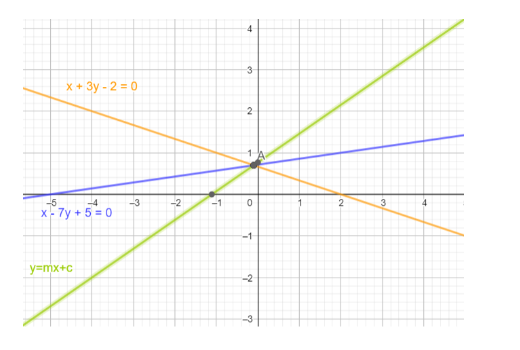
We know that the slope of the line ax+by+c = 0 is given by $m=\dfrac{-a}{b}$
Hence, we have
Slope of the line x-7y+5 = 0 is $\dfrac{-1}{-7}=\dfrac{1}{7}$ and the slope of the line x+3y -2 = 0 is $\dfrac{-1}{3}$
We know that the angle between two lines of slopes ${{m}_{1}}$ and ${{m}_{2}}$ is given by $\phi ={{\tan }^{-1}}\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right|$
Hence, we have
Angle between the lines x-7y+5 = 0 and x+3y -2 = 0 is $\phi ={{\tan }^{-1}}\left| \dfrac{\dfrac{1}{7}-\left( -\dfrac{1}{3} \right)}{1+\left( \dfrac{1}{7} \right)\left( \dfrac{-1}{3} \right)} \right|={{\tan }^{-1}}\left| \dfrac{10}{21-1} \right|={{\tan }^{-1}}\left( \dfrac{1}{2} \right)$
Also, we have
Angle between the lines x-7y+5 and y = mx+c is given by
$\theta ={{\tan }^{-1}}\left| \dfrac{m-\dfrac{1}{7}}{1+\dfrac{m}{7}} \right|={{\tan }^{-1}}\left| \dfrac{7m-1}{m+7} \right|$
But since the line x-7y+5 = 0 is the angle bisector of the lines x+3y-2 =0 and y = mx+c, we have
$\phi =\theta $
Hence, we have
${{\tan }^{-1}}\left| \dfrac{7m-1}{m+7} \right|={{\tan }^{-1}}\left| \dfrac{1}{2} \right|$
Since ${{\tan }^{-1}}x$ is one-one, we have
$\left| \dfrac{7m-1}{m+7} \right|=\dfrac{1}{2}$
We know that if $\left| x \right|=a,a\ge 0,$ then $x=\pm a$
Hence, we have
$\dfrac{7m-1}{m+7}=\pm \dfrac{1}{2}$
Taking the positive sign, we get
$\dfrac{7m-1}{m+7}=\dfrac{1}{2}$
Cross multiplying, we get
$14m-2=m+7$
Hence, we have
$13m=9\Rightarrow m=\dfrac{9}{13}$
Taking the negative sign, we get
$\dfrac{7m-1}{m+7}=\dfrac{-1}{2}$
Cross multiplying, we get
$14m-2=-m-7$
Hence, we have
$15m=-5\Rightarrow m=\dfrac{-1}{3}$
Finding the coordinates of point of intersection of x+3y- 2 = 0 and x-7y+5 = 0
We have
x+3y -2 = 0 (i)
x-7y+5=0 (ii)
Subtracting equation (i) from equation (ii), we get
$-10y+7=0\Rightarrow y=\dfrac{7}{10}$
Substituting the value of y in equation (ii), we get
$\begin{align}
  & x-\dfrac{49}{10}+5=0 \\
 & \Rightarrow x=\dfrac{-1}{10} \\
\end{align}$
Hence, we have $A\equiv \left( \dfrac{-1}{10},\dfrac{7}{10} \right)$
When $m=\dfrac{9}{13}$, we have
Equation of the line is ‘$y=\dfrac{9}{13}x+c$
Since the line passes through A, we have
$\begin{align}
  & \dfrac{7}{10}=\dfrac{-9}{130}+c \\
 & \Rightarrow c=\dfrac{91+9}{130}=\dfrac{10}{13} \\
\end{align}$
Hence, the equation of the line is
$y=\dfrac{9}{13}x+\dfrac{10}{13}$
Multiplying both sides by 13, we get
$13y=9x+10$
When $m=\dfrac{-1}{3}$, we have
Equation of the line is $y=-\dfrac{1}{3}x+c$
Since the line passes through A, we have
$\begin{align}
  & \dfrac{7}{10}=\dfrac{1}{30}+c \\
 & \Rightarrow c=\dfrac{21-1}{30}=\dfrac{2}{3} \\
\end{align}$
Hence, the equation of the line is
$y=\dfrac{-1}{3}x+\dfrac{2}{3}$
Multiplying both sides by 3, we get
$3y=-x+2$
This is the same as equation (i) and hence is rejected.
Hence the equation of the line is $13y=9x+10$

Note: Alternative solution:
We know that the equation of the line which is concurrent to two lines ${{L}_{1}}=0$ and ${{L}_{2}}=0$ is given by ${{L}_{1}}+{{L}_{2}}=0$
Hence, we have
Equation of the line is
$\begin{align}
  & x+3y-2+\left( x-7y+5 \right)=0 \\
 & \Rightarrow x\left( 1+ \right)+y\left( 3-7 \right)-2+5=0 \\
\end{align}$
Since the slope of the line is $\dfrac{9}{13}$(Proved above), we have
$\begin{align}
  & -\dfrac{1+}{3-7}=\dfrac{9}{13} \\
 & \Rightarrow 13+13=63-27 \\
 & \Rightarrow 50=40 \\
 & \Rightarrow =\dfrac{4}{5} \\
\end{align}$
Hence the equation of the line is
$\begin{align}
  & x\left( 1+\dfrac{4}{5} \right)+y\left( 3-7\dfrac{4}{5} \right)-2+5\left( \dfrac{4}{5} \right)=0 \\
 & \Rightarrow 9x-13y+10=0 \\
\end{align}$
which is the same as obtained above.