Question

The line segments joining the mid-point M and N are parallel sides AB and DC respectively of a trapezium ABCD is perpendicular to both the sides AB and DC. Prove that $ AD = BC $ .

Answer 1

Hint: For two triangles $ \Delta ABC $ and $ \Delta DEF $ , if it is given that $ AB = DE $ , $ BC = EF $ and $ \angle ABC = \angle DEF $ , then by the side-angle-side property, both the triangles $ \Delta ABC $ and $ \Delta DEF $ are congruent to each other and can be written as $ \Delta ABC \cong \Delta DEF $ .

Complete step by step answer:
We are given the trapezium ABCD such that the line segments joining the mid-point M and N are parallel sides AB and DC respectively and are perpendicular to both the sides AB and DC.
So, we get that \[\angle AMN = \angle BMN = \angle DNM = \angle CNM = {90^o}\]
Construct two lines AN by joining the points A and N, and construct another line BN by joining B and N. It can be shown in the given figure:

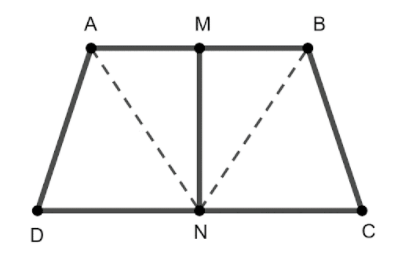
Consider the triangle $ \Delta AMN $ and $ \Delta BMN $
Since by the construction, both these triangles are right angles triangle such that
 $ \angle AMN = \angle BMN = {90^o} $
Also, it is given that M is the midpoint of AB, hence
 $ AM = MB $
And the side MN is common in both triangles.
Hence, we can say that using the side-angle-side congruence rule $ \Delta AMN $ and $ \Delta BMN $ are congruent to each other.
Since the triangle $ \Delta AMN $ and $ \Delta BMN $ are congruent, then following statements be written for all the sides and angles,
 $
  1)AM = BM \\
  2)AN = BN \\
  3)MN = MN \\
  4)\angle MAN = \angle MBN \\
  5)\angle AMN = \angle BMN \\
  6)\angle ANM = \angle BNM \\
  $
Now consider the triangle $ \Delta ADN $ and $ \Delta BCN $ ,
It is given in the question that N is the mid-point of the side DC, so we can write
 $ DN = CN $
Since the $ \Delta AMN $ and $ \Delta BMN $ are congruent, then from the above listed statement for the given congruent triangles, we have the second statement that
 $ AN = BN $
Also , from the sixth statement we can write,
 $ \angle ANM = \angle BNM $ ---(7)
By the construction we know that the line joining the point M and N, is perpendicular to both Ab and CD. So we get,
 $ \angle MND = \angle MNC = {90^o} $ ----(8)
From the statement (7) and (8) , since the subtraction of equal angles from the equal angles is also equal, we will subtract angles in equation (7) from angles in equation (8).
 $ \angle MND - \angle ANM = \angle MNC - \angle BNM $
Since $ \angle MND = \angle MNC = {90^o} $
From the given figure of the trapezium we can write
 $ \angle MND - \angle ANM = \angle AND $ and $ \angle MNC - \angle BNM = \angle BNC $
Substitute the above angles in the equality $ \angle MND - \angle ANM = \angle MNC - \angle BNM $ , we get
 $ \angle AND = \angle BNC $
So for $ \Delta ADN $ and $ \Delta BCN $ , we have
 $ DN = CN $
 $ AN = BN $
 $ \angle AND = \angle BNC $
Hence, we can say that using the side-angle-side congruence rule $ \Delta ADN $ and $ \Delta BCN $ are congruent to each other.
Since, we get $ \Delta ADN \cong \Delta BCN $ so we can infer that the side AD of $ \Delta ADN $ is equal to side BC in $ \Delta BCN $ .
Hence we get , $ AD = BC $

Note:
 It is given that triangles $ \Delta ABC $ and $ \Delta DEF $ are congruent to each other and can be written as $ \Delta ABC \cong \Delta DEF $ then we can infer the following equalities,
 $
  AB = DE \\
  AC = DF \\
  BC = EF \\
  \angle ABC = \angle DEF \\
  \angle ACB = \angle DFE \\
  \angle BAC = \angle EDF \\
  $