Question

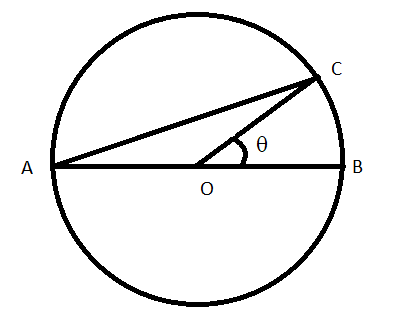
The line AB is the diameter of a circle; centre O. C is the point on a circumference such that $\angle COB=\theta $. The area of the minor segment cut off by AC is equal to twice, the area of sector BOC. Find whether the statement $\sin \dfrac{\theta }{2}\cos \dfrac{\theta }{2}=\pi \left( \dfrac{1}{2}-\dfrac{\theta }{120} \right)$ is true or false.

A. true B. false

Answer 1

Hint:We have been the relation between the two areas. Using the properties of an area of a segment of a circle with a certain angle we find the equation. We consider the smaller areas as the area covered under the curve. We also need to use properties of the triangle to find a certain area of a triangle. From the relation, we find out the given statement.

Complete step by step answer:

We need to find the area of a different part of the circle under different arcs.
The area of the minor segment cut off by AC is the area covered by smaller $\overset\frown{AC}$.
The area of sector BOC is also covered by smaller $\overset\frown{BC}$.
Let the radius of the circle be r unit. So, $AO=OB=OC=r$.
The total area of the circle is $A=\pi {{r}^{2}}$ sq. unit.
Every arc makes a certain angle at the centre made by the two endpoints of the arc and the centre. For example, smaller $\overset\frown{BC}$ makes angle $\theta $ at the centre which means $\angle COB=\theta $.
We can find the area created by every arc using its angle made at the centre.
The formula for the area is $\dfrac{angle\times A}{2\pi }$ as $2\pi $ is total angle of the circle at the centre which defines the total area also.
The area of sector BOC = smaller $\overset\frown{BC}$ = $\dfrac{\theta \times A}{2\pi }=\dfrac{A\theta }{2\pi }$.
Now the area of the minor segment cut off by AC = $\overset\frown{AC}-\Delta AOC$. Here $\Delta AOC$ defines its area.
We need to find the angle of $\overset\frown{AC}$. Let it be $\alpha $.
So, $\angle COB=\theta $. $\angle AOC=\alpha $ and $\angle COB+\angle AOC=\theta +\alpha =\pi $.
Solving the equation, we get value of $\alpha $ with respect to $\theta $ which is $\alpha =\pi -\theta $.
The area of the minor segment cut off by AC = $\dfrac{\left( \pi -\theta \right)\times A}{2\pi }-\Delta AOC$.
Now we find the area of $\Delta AOC$ by using properties of triangle which tells us
area of $\Delta AOC$ = $\dfrac{1}{2}\times \left| \overline{AO} \right|\times \left| \overline{OC} \right|\times \sin \left( \angle AOC \right)$.
We put the values to get area of $\Delta AOC$ = $\dfrac{1}{2}\times r\times r\times \sin \left( \pi -\theta \right)=\dfrac{{{r}^{2}}\sin \theta }{2}$.
So, the area of the minor segment cut off by AC = $\dfrac{\left( \pi -\theta \right)\times A}{2\pi }-\dfrac{{{r}^{2}}\sin \theta }{2}$.
We have been given that the area of the minor segment cut off by AC is equal to twice, the area of sector BOC.
The equation becomes $\dfrac{\left( \pi -\theta \right)\times A}{2\pi }-\dfrac{{{r}^{2}}\sin \theta }{2}=2\times \dfrac{A\theta }{2\pi }$.
We solve the equation
\[\begin{align}
  & \dfrac{\left( \pi -\theta \right)\times A}{2\pi }-\dfrac{{{r}^{2}}\sin \theta }{2}=2\times \dfrac{A\theta }{2\pi } \\
 & \Rightarrow \dfrac{{{r}^{2}}\sin \theta }{2}=\dfrac{\left( \pi -\theta \right)\times A}{2\pi }-\dfrac{2A\theta }{2\pi }=\dfrac{\left( \pi -3\theta \right)\times A}{2\pi } \\
\end{align}\]
We put value $A=\pi {{r}^{2}}$.
\[\begin{align}
  & {{r}^{2}}\sin \theta =\dfrac{\left( \pi -3\theta \right)\times A}{\pi }=\dfrac{\left( \pi -3\theta \right)\times \pi {{r}^{2}}}{\pi } \\
 & \Rightarrow \sin \theta =\pi -3\theta \\
 & \Rightarrow 2\sin \dfrac{\theta }{2}\cos \dfrac{\theta }{2}=\pi -3\theta \\
 & \Rightarrow \sin \dfrac{\theta }{2}\cos \dfrac{\theta }{2}=\dfrac{\pi -3\theta }{2}=\pi \left( \dfrac{1}{2}-\dfrac{3\theta }{2\pi } \right)=\pi \left( \dfrac{1}{2}-\dfrac{\theta }{\dfrac{2\pi }{3}} \right)=\pi \left( \dfrac{1}{2}-\dfrac{\theta }{120} \right) \\
\end{align}\]
Thus, we prove the given statement is true. So, the correct option is (A).

Note:
 Although from the figure we might confuse the area of $\overset\frown{AC}$ with the area cut off by line AC. One is the area under the arc and the other one is the area under chord AC. That’s why we had to omit the area of $\Delta AOC$. At the end, we made some changes in the answer to match it with the given statement.