Question

The length of two parallel sides of a trapezium is $10\,cm$ and $15\,cm$. The lengths of the other two sides are $4\,cm$ and $6\,cm$. How will you find out the area and magnitudes of $4$ angles of the trapezium?

Answer 1

Hint: In this question, we need to evaluate the area and the angles of the trapezium such that the parallel sides of trapezium are $10\,cm$ and $15\,cm$. For this we will use the relation between sides and the height of the trapezium.

Complete step by step answer:
In the given question, first we will draw two perpendiculars from the side of $10\,cm$ to its opposite parallel side. Therefore, the length between these two perpendiculars is $10\,cm$.

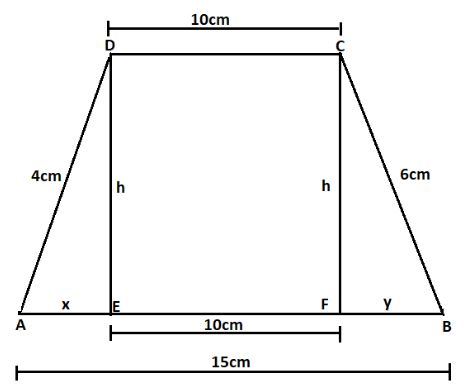
We know that, $AB = 15cm$$ \Rightarrow {y^2} + {h^2} = 36 - - - - \left( 2 \right)$
Therefore,
$ \Rightarrow x + y + 10 = 15$
$ \Rightarrow x + y = 15 - 10$
$ \Rightarrow x + y = 5$

Now, using Pythagoras theorem in $\vartriangle AED$
$ \Rightarrow A{D^2} = A{E^2} + E{D^2}$
We know that $AD = 4cm$
$ \Rightarrow {x^2} + {h^2} = 16 - - - - \left( 1 \right)$
Now, using Pythagoras theorem in $\vartriangle BCF$
$ \Rightarrow B{F^2} + C{F^2} = B{C^2}$
Now, subtracting $1$ from $2$.
We get,
$ \Rightarrow {y^2} - {x^2} = 36 - 16$
$ \Rightarrow {y^2} - {x^2} = 20$
$ \Rightarrow \left( {y - x} \right)\left( {y + x} \right) = 20$

Now using the equation, $x + y = 5 - - - - \left( 3 \right)$
$ \Rightarrow \left( {y - x} \right)5 = 20$
Now divide both sides by $5$
$ \Rightarrow y - x = 4 - - - - \left( 4 \right)$
Now adding equation $3\,and\,4$
$ \Rightarrow x + y + y - x = 5 + 4$
$ \Rightarrow 2y = 9$
$ \Rightarrow y = \dfrac{9}{2}cm$
Now, we will put the value of y in equation $3$
$ \Rightarrow x + \dfrac{9}{2} = 5$
$ \Rightarrow x = \dfrac{1}{2}cm$

Now, putting the value of $x$ in the equation is $1$ .
$ \Rightarrow {\dfrac{1}{2}^2} + {h^2} = 16$
$ \Rightarrow {h^2} = 16 - \dfrac{1}{4}$
$ \Rightarrow {h^2} = \dfrac{{63}}{4}$
Taking square root both sides,
$ \Rightarrow h = \sqrt {\dfrac{{63}}{4}} = \dfrac{{3\sqrt 7 }}{2}cm$
We know that the area of trapezium is the product of the sum of parallel sides and its height.Therefore,
Area of trapezium $ = \dfrac{1}{2} \times \left( {AB + CD} \right) \times h$
$ \Rightarrow \dfrac{1}{2} \times 25 \times \dfrac{{3\sqrt 7 }}{2}$
$ \Rightarrow \dfrac{{75\sqrt 7 }}{4}c{m^2}$
Therefore, the area of trapezium is $\dfrac{{75\sqrt 7 }}{4}c{m^2}$.

Now in $\vartriangle AED$
$ \Rightarrow \tan A = \dfrac{h}{x}$
$ \Rightarrow \tan A = \dfrac{{\dfrac{{3\sqrt 7 }}{2}}}{{\dfrac{1}{2}}}$
$ \Rightarrow \tan A = 3\sqrt 7 $
$ \Rightarrow \angle A = {\tan ^{ - 1}}3\sqrt 7 $
 $\angle ADE = 90 - A$
$ \Rightarrow \angle ADE = 90 - {\tan ^{ - 1}}3\sqrt 7 $
$ \Rightarrow \angle D = 90 + 90 - {\tan ^{ - 1}}3\sqrt 7 $
$ \Rightarrow \angle D = 180 - {\tan ^{ - 1}}3\sqrt 7 $

Similarly, now in $\vartriangle BCF$
$ \Rightarrow \tan B = \dfrac{h}{y}$
$ \Rightarrow \tan B = \dfrac{{\dfrac{{3\sqrt 7 }}{2}}}{{\dfrac{9}{2}}}$
$ \Rightarrow \tan B = \dfrac{{\sqrt 7 }}{3}$
$ \Rightarrow \angle B = {\tan ^{ - 1}}\dfrac{{\sqrt 7 }}{3}$
 $\angle BCF = 90 - B$
$ \Rightarrow \angle BCF = 90 - {\tan ^{ - 1}}\dfrac{{\sqrt 7 }}{3}$
$ \Rightarrow \angle C = 90 + 90 - {\tan ^{ - 1}}\dfrac{{\sqrt 7 }}{3}$
$ \therefore \angle C = 180 - {\tan ^{ - 1}}\dfrac{{\sqrt 7 }}{3}$

Therefore, $\angle A\,,\,\angle B\,,\,\angle C\,and\,\angle D$ are ${\tan ^{ - 1}}3\sqrt 7 $ , ${\tan ^{ - 1}}\dfrac{{\sqrt 7 }}{3}$, $180 - {\tan ^{ - 1}}\dfrac{{\sqrt 7 }}{3}$and $180 - {\tan ^{ - 1}}3\sqrt 7 $.

Note: There are some properties of trapezium like the bases of a trapezium(isosceles) are parallel to each other. The length of both the diagonals is equal. The diagonals of a trapezium always intersect each other. The adjacent interior angles in a trapezium sum up to be \[180^\circ .\] The sum of all the interior angles in a trapezium is always \[360^\circ .\]