Question

The length of the transverse common tangent of the circles ${{x}^{2}}+{{y}^{2}}-2x+4y+4=0$ and ${{x}^{2}}+{{y}^{2}}+4x-2y+1=0$ is:
(a)$\sqrt{17}$ units
(b)3 units
(c)9 units
(d)$\sqrt{15}$ units

Answer 1

Hint: By using the general equation of circle, we find the coordinates of center and radius for the given circles. After that we determine the distance between two circles. By using all these values, we can evaluate the length of the transverse common tangent.

Complete step-by-step answer:
From the general equation of circle $a{{x}^{2}}+b{{y}^{2}}+2gx+2fy+c=0$ where a, b, c, g and f are constants. The coordinates of center are defined as (-g, -f) and the radius is defined as $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$.
Now, using the general equation we can find the coordinates of center and radius for the equation of circle given in the problem statement.
The equation of first circle, let E1: ${{x}^{2}}+{{y}^{2}}-2x+4y+4=0$ where g = -1, f = 2 and c = 4.
So, the coordinate of the first circle is: ${{C}_{1}}=\left( 1,-2 \right)$ and radius of the circle: ${{r}_{1}}=1$.
Now, the equation of second circle, let E2:${{x}^{2}}+{{y}^{2}}+4x-2y+1=0$ where g = 2, f = -1 and c = 1.
So, the coordinate of this circle is: ${{C}_{2}}=\left( -2,1 \right)$ and the radius of the circle:${{r}_{2}}=2$.
So, diagrammatically the condition of tangent can be shown as:

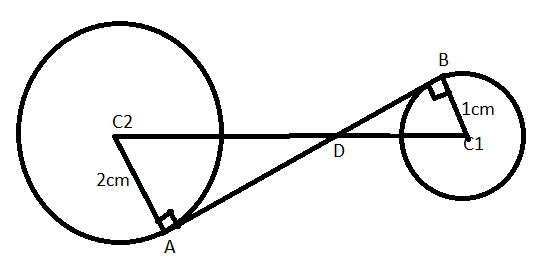
Now, we have to find the distance between two circles i.e. d,
By using the distance formula between two points (a, b) and (c, d): $d=\sqrt{{{(a-c)}^{2}}+{{(b-d)}^{2}}}$
So, the distance between (1, -2) and (-2, 1) will be:
$\begin{align}
  & d=\sqrt{{{\left( 1-(-2) \right)}^{2}}+{{(-2-1)}^{2}}} \\
 & d=\sqrt{{{(3)}^{2}}+{{(-3)}^{2}}} \\
 & d=\sqrt{9+9}=3\sqrt{2} \\
 & d={{C}_{1}}{{C}_{2}}=3\sqrt{2} \\
\end{align}$
So, distance between the circles is greater than the sum of both the radii of circle,
$\because d>{{r}_{1}}+{{r}_{2}}$
Therefore, E1 and E2 are not intersecting each other.
The length of transverse common tangent can be expressed as:
 $L=\sqrt{{{d}^{2}}-{{\left( {{r}_{1}}+{{r}_{2}} \right)}^{2}}}$
By putting values in the above expression, we get
$\begin{align}
  & L=\sqrt{{{\left( 3\sqrt{2} \right)}^{2}}-9} \\
 & L=\sqrt{9}=3units \\
\end{align}$
Hence, the length of the transverse common tangent is 3units.
Therefore, option (b) is correct.

Note: The key concept for solving this question is the knowledge of the general equation of a circle and its various associated parameters. It is a direct question so by putting the values we get the desired answer. This knowledge is helpful in solving complex problems.