Question

The length of the shadow of a vertical pole 9 m high, when the sun’s altitude is \[30^\circ \], is ( in cm ) :
a)\[{\text{3}}\sqrt {\text{3}} \]
b)\[9\]
c)\[9\sqrt 3 \]
d)\[18\sqrt 3 \]

Answer 1

Hint: In this question we use the \[{{tan\theta = }}\dfrac{{{\text{perpendicular}}}}{{{\text{base}}}}\], where \[\theta \] be the angle between the base and the hypotenuse of a right angle triangle and \[\tan 30^\circ = \dfrac{1}{{\sqrt 3 }}\].

Complete step-by-step answer:

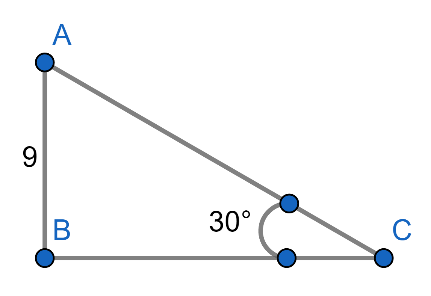
Let, AB be the vertical pole whose height is 9 m and BC be the length of the shadow, which is required.
Here, it is given that the sun’s altitude is \[30^\circ \].
Now, we know that \[{{tan\theta = }}\dfrac{{{\text{perpendicular}}}}{{{\text{base}}}}\], where \[\theta \] be the angle between the base and the hypotenuse of a right angle triangle.
\[\therefore \]Therefore, from the triangle \[\vartriangle \]ABC, we write
\[ \tan \theta = \dfrac{{AB}}{{BC}}\left[ {where{{ }}AB = perpendicular{{ }} \& {{ }}BC = base} \right] \\
   \Rightarrow \tan 30^\circ = \dfrac{9}{{BC}}\left[ {\because \theta = 30^\circ } \right] \\
   \Rightarrow BC = \dfrac{9}{{\tan 30^\circ }} \\
   \Rightarrow BC = 9\cot 30^\circ = 9\sqrt 3 \left[ \begin{gathered}
  \because \tan 30^\circ = \dfrac{1}{{\sqrt 3 }} \\
  \therefore \cot 30^\circ = \dfrac{1}{{\tan 30^\circ }} = \sqrt 3 \\
\end{gathered} \right] \\
\]
So, the length of the shadow is \[9\sqrt 3 {\text{ }}m\].
Note: Here, you have to draw a clear diagram at the time of solving this type of height & distance problems.
After that, you have to know the properties of triangles and the trigonometric ratios.