Question

The length of the shadow of a tree$7m$high, when the sun’s elevation is \[{{45}^{0}}\], is:
A) $7m$
B) \[3.5m\]
C) \[5m\]\[\]
D) \[14m\]

Answer 1

Hint: We will draw the figure as per the given word statement in the questions. Use properties of different trigonometric functions. Note down the known values and unknown terms and find correlation between the two. Hence, here we take the tangent ratio and its values to find the length of the tree.

Complete answer
First, we draw the figure with given data.

Here \[AB\text{ }=~7m\](height of tree)

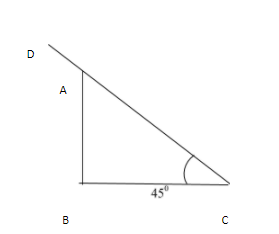
Angle \[C\text{ }={{45}^{0}}\](angle of elevation) A
We need to find \[BC\] (length of shadow)
\[D\] = Point of elevation (Sun)
     \[{{45}^{0}}\]

Here \[AB\] can be considered as perpendicular to the Right triangle ABC and \[BC\] can be the base of the triangle ABC.
Hence the required ratio is \[tan\]and angle is \[{{45}^{0}}\].
So, \[\tan \theta =\dfrac{perpendicular}{base}=\dfrac{AB}{BC}\]
Put known values,
\[\Rightarrow \tan {{45}^{0}}=\dfrac{7m}{BC}\]
As we know that, $\tan 45{}^\circ =1$
\[\Rightarrow 1=\dfrac{7m}{BC}\]
Applying cross multiplication:
\[1\times BC=7m\]
The length of the shadow of a tree$7m$high, when the sun’s elevation is\[{{45}^{0}}\], is $=7m$
Hence, from the given multiple options, option A is the correct answer.

Note: In these types of height and distance problems, we need to first draw the figure then place the values (dimensions) given in the problem correctly. We need to be very keen to choose the correct ratio, the correct and applicable trigonometric function and its relation with the proper angle. The assign values against the angle and the segments and solve it accordingly.