Question

The length of the shadow of a tower on a level plane is found to be 2k meters longer when the sun’s altitude is $30{}^\circ $ than when it was $45{}^\circ $ . Prove that the height of the tower is $k\left( \sqrt{3}+1 \right)$ meters.

Answer 1

Hint: Assume that the height of the tower from the ground is ‘h’. First, draw a rough diagram of the given conditions and then use the formula $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}$ in the different right angle triangles and substitute the given values to get the height.

Complete step-by-step answer:

Let us start with the question by drawing a representative diagram of the situation given in the question.

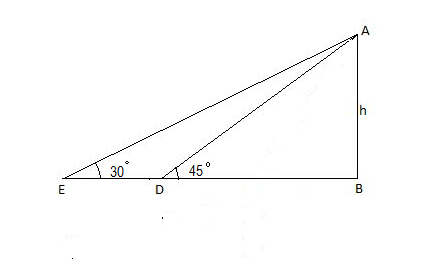
According to the above figure:
We have assumed the height of the tower from the ground as ‘h’. Therefore, AB = h. Also, assume that the distance BD is ‘x’ meters and distance BE is ‘y’ meters.

Now, in right angle triangle ADB,
$\angle ADB=45{}^\circ $

We know that, $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}$. Therefore,

$\begin{align}
  & \tan 45{}^\circ =\dfrac{AB}{BD} \\
 & \Rightarrow \tan 45{}^\circ =\dfrac{h}{x} \\
 & \Rightarrow x=\dfrac{h}{\tan 45{}^\circ } \\
\end{align}$

And we know that the value of $\tan 45{}^\circ $ is equal to 1.
$\therefore x=h.............(i)$

Now, in right angle triangle AEB,

\[\angle AEB=\beta \]

We know that, $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}$. Therefore,

$\begin{align}

  & \tan 30{}^\circ =\dfrac{AB}{BE} \\

 & \Rightarrow \tan 30{}^\circ =\dfrac{h}{y} \\

 & \Rightarrow y=\dfrac{h}{\tan 30{}^\circ } \\

\end{align}$

And we know that the value of $\tan 30{}^\circ $ is equal to $\dfrac{1}{\sqrt{3}}$ .

$\therefore y=\sqrt{3}h.............(ii)$

Now according to the data given in the question:

BE-BD=2k

$\Rightarrow y-x=2k$

Now we will substitute x and y from equation (i) and equation (ii), respectively. On doing so, we get

$\sqrt{3}h-h=2k$

$\Rightarrow h=\dfrac{2k}{\sqrt{3}-1}$

Now we will multiply and divide the right-hand side of the equation with $\sqrt{3}+1$ . On doing so, we get

$h=\dfrac{2k\left( \sqrt{3}+1 \right)}{\left( \sqrt{3}+1 \right)\left( \sqrt{3}-1 \right)}$

$\Rightarrow h=\dfrac{2k\left( \sqrt{3}+1 \right)}{3-1}=\dfrac{k\left( \sqrt{3}+1 \right)}{{}}=k\left( \sqrt{3}+1 \right)$

So, the height of the tower is $k\left( \sqrt{3}+1 \right)$ meters. Hence, we have proved the part asked in the question.

Note: Do not use any other trigonometric function like sine or cosine of the given angle because the information which is provided to us is related to the base of the triangle, and we have to find the height. So, the length of the hypotenuse is of no use. Therefore, the formula of the tangent of the angle is used. We can use sine or cosine of the given angles but then the process of finding the height will be lengthy.