Question

The length of the parallel sides of a trapezium in the ratio \[4:7\]. If the height of the trapezium is \[14m\] and its area is \[385\text{ }sq.\text{ }m\], find the length of its parallel sides.

Answer 1

Hint: Here first we will use the formula of the area of the trapezium and its properties to find the unknown length of the parallel sides.
Area of trapezium is = \[\dfrac{1}{2}\times \left( \text{sum of parallel sides} \right)\times height\].
Also, we will assume the ratio be \[x\] and hence we will have non-parallel sides in terms of \[x\].

Complete step-by- step solution:
With the reference to the figure given below -

             

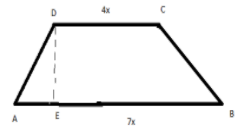
Let us suppose that “x” is the common factor in the given ratio.
Then the length of the parallel sides be \[7x\text{ }and\text{ }4xcm\].
Give Area$=385\ sq.m$
Now, Area of trapezium = \[\dfrac{1}{2}\times \left( \text{sum of parallel sides} \right)\times height\]
Put Known Values in the above equation we get
$\Rightarrow 385=\dfrac{1}{2}\times \left( 4x+7x \right)\times 14$
$\begin{align}
 &\Rightarrow \dfrac{385\times 2}{14}=11x \\
 &\Rightarrow 55=11x \\
 &\therefore \text{ x=5} \\
\end{align}$
Put $x=5$
Hence, the length of the parallel sides is –
$\begin{align}
 &\Rightarrow 7x=7\times 5 \\
 &\Rightarrow 7x=35m \\
 & and \\
 &\Rightarrow 4x=4\times 5 \\
 &\Rightarrow 4x = 20m \\
\end{align}$
Hence, the length of its parallel sides is $20m\text{ and 35m}$

Note: Trapezium is the quadrilateral and 2- dimensional shape which has only the two parallel sides and the other two sides are non-parallel. It consists of four vertices and four edges. Perimeter of trapezium is equal to the sum of the length of all the four sides. In these types of problems it is better to draw the figure. So, that - we can relate the given quantity to the concerned part of the shape. Here we need to check whether all the given quantities are in the same unit or needed to change.