Question

The length of the minute hand of a clock is 14 cm. Find the area swept by a minute hand in 5 minutes.

Answer 1

Hint: Here, we can use the concept that when the minute hand of the clock rotates, it circularly sweeps the area. When the minute hand of the clock completes one complete rotation, it sweeps the total area of a circle with radius equal to the length of the minute hand. So, for 60 minutes (one complete rotation), it sweeps the area of the circle. So, for 5 minutes it will be one-twelfth of the total area.

Complete step-by-step answer:
Here, we have a minute hand of a clock whose length is 14 cm. We need to find the area swept by the minute hand of the clock in 5 minutes. One complete rotation will sweep the circle fully with the radius of the circle being equal to the length of a minute hand in 60 minutes.

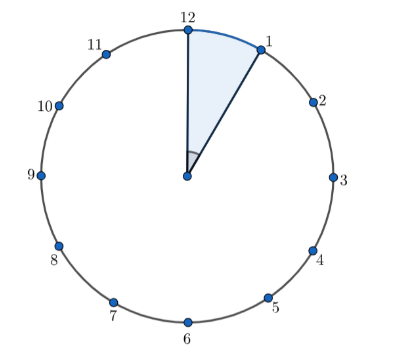
We know that the period for one complete rotation of a minute hand is 60 minutes. So, the area swept by the minute hand of the clock in 60 minutes can be calculated using the formula:
$Area=\pi {{r}^{2}}$
$\Rightarrow Area=\pi \left( 14c{{m}^{2}} \right)$
Using the value $\pi =\dfrac{22}{7}$ , we get :
$\Rightarrow Area=\dfrac{22}{7}\left( 14c{{m}^{2}} \right)=22\times 2\times 14=616c{{m}^{2}}$
So, the total area swept in 60 min is 616 sq. cm. So, the area swept in one minute is given by $\dfrac{616}{60}$ sq. cm.
So, we can calculate the area swept in 5 minutes by multiplying the above result with 5.
$Area=\dfrac{616}{60}\times 5=51.3333c{{m}^{2}}$
Hence, we get the answer as 51.3333 sq. cm.

Note: We can directly calculate the area swept by minute hand in x minute using the formula:
$Area=\dfrac{x}{60}\times \pi {{l}^{2}}$
Here, l is the length of the minute hand. Also, while doing calculations, take care of the units. Mathematical operations can only be performed if units are the same.