Question

The length of the latus rectum of the hyperbola $xy-3x-3y+7=0$ is
(A) 4
(B) 3
(C) 2
(D) 1

Answer 1

Hint: We solve this question by first considering the given equation of the hyperbola. Then we simplify the equation of the parabola by factorization. Then we realize that it is similar to the equation of the rectangular hyperbola. Then we consider the formula for the length of the latus rectum of the rectangular hyperbola $xy={{c}^{2}}$, Length of latus rectum is equal to $2\sqrt{2}c$. Using it we can find the value of the length of the latus rectum of our parabola.

Complete step-by-step solution:
The given equation of the hyperbola is $xy-3x-3y+7=0$.
First let us simplify it by factorization.
$\begin{align}
  & \Rightarrow xy-3x-3y+7=0 \\
 & \Rightarrow x\left( y-3 \right)-3y+7=0 \\
\end{align}$
Let us add 9 on both sides of the above equation.
$\begin{align}
  & \Rightarrow x\left( y-3 \right)-3y+9+7=9 \\
 & \Rightarrow x\left( y-3 \right)-3\left( y-3 \right)+7=9 \\
 & \Rightarrow \left( x-3 \right)\left( y-3 \right)+7=9 \\
 & \Rightarrow \left( x-3 \right)\left( y-3 \right)=9-7 \\
 & \Rightarrow \left( x-3 \right)\left( y-3 \right)=2 \\
\end{align}$
We can see that the above equation is similar to the equation of the rectangular hyperbola, $xy={{c}^{2}}$.
By comparing this general equation of rectangular hyperbola with the obtained equation, we can see that,
$\begin{align}
 & \Rightarrow {{c}^{2}}=2 \\
 & \Rightarrow c=\sqrt{2} \\
\end{align}$
Now let us consider the formula for the length of the latus rectum of the hyperbola $xy={{c}^{2}}$ is $2\sqrt{2}c$.
So, the length of the latus rectum of the hyperbola, $\left( x-3 \right)\left( y-3 \right)=2$ can be given as,
$\begin{align}
  & \Rightarrow 2\sqrt{2}\times \sqrt{2} \\
 & \Rightarrow 2\times 2 \\
 & \Rightarrow 4 \\
\end{align}$

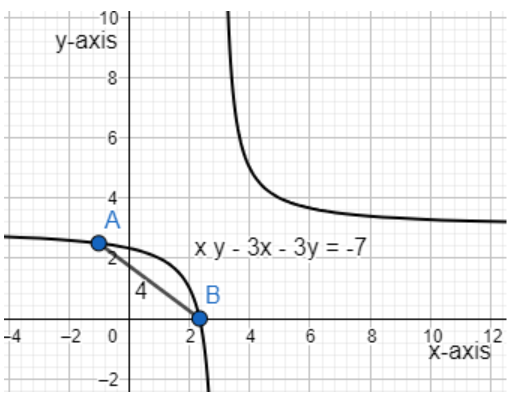
So, we get the length of the latus rectum of the hyperbola, $\left( x-3 \right)\left( y-3 \right)=2$ as 4. Hence the answer is Option A.

Note: The common mistake one makes while solving this problem is one might take the formula for the length of the latus rectum of the rectangular parabola $xy={{c}^{2}}$ as $\sqrt{2}c$. But that is the length of the semi latus rectum not for the latus rectum. So, for the latus rectum, it is double the length of the semi latus rectum, which is $2\sqrt{2}c$.