Question

The length of the garden is $5m$ longer than its width and the area is $14{{m}^{2}}$. How long is the garden?

Answer 1

Hint: The measurement of the garden is given in terms of its length as well as width. Thus, we understand that the garden is rectangular in shape. We shall use the given relation and develop a quadratic equation in terms of the width and further solve it to find the length and breadth of the garden.

Complete step-by-step answer:
Let the length of the garden be $l$ meters and let the width of the garden be $b$meters.
Given that the length of the garden is $5m$ longer than its width

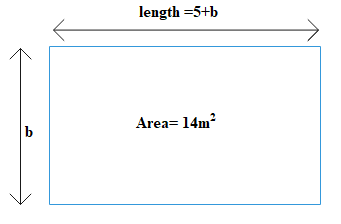
$\Rightarrow l=5+b$ ……………………. Equation (1)
And the area is $14{{m}^{2}}$.
The area of a rectangle is given as its length multiplied by its width
$\Rightarrow A=l\times b$
$\Rightarrow 14=l\times b$
From equation (1),
  $\begin{align}
  & \Rightarrow 14=\left( 5+b \right)\times b \\
 & \Rightarrow 14=5b+{{b}^{2}} \\
 & \Rightarrow {{b}^{2}}+5b-14=0 \\
\end{align}$
For any quadratic equation $a{{x}^{2}}+bx+c=0$,
the sum of the roots $=-\dfrac{b}{a}$ and the product of the roots $=\dfrac{c}{a}$.
Thus, for the equation, ${{b}^{2}}+5b-14=0$,
We will find numbers by hit and trial whose product is equal to $1\times \left( -14 \right)=-14$ and whose sum is equal to $5$.
Such two numbers are 7 and -2 as $7+\left( -2 \right)=5$ and $7\times \left( -2 \right)=-14$.
Now, factoring the equation:
$\Rightarrow {{b}^{2}}+7b-2b-14=0$
Taking common, we get:
$\begin{align}
  & \Rightarrow b\left( b+7 \right)-2\left( b+7 \right)=0 \\
 & \Rightarrow \left( b+7 \right)\left( b-2 \right)=0 \\
\end{align}$
Hence, $b+7=0$ or $b-2=0$
$\Rightarrow b=-7$ or $b=2$
Therefore, the roots of the equation are $b=-7,2$.
Since the measurement of length cannot be negative, we ignore the value $b=-7$and take $b=2$.
Therefore, the measurement of width is equal to $2m$.
Again, using equation (1), we get
$\begin{align}
  & l=b+5 \\
 & \Rightarrow l=2+5 \\
 & \Rightarrow l=7m \\
\end{align}$
Therefore, the length of the garden is 7 meters.

Note:
We encounter such geometrical things in our day-to-day life. Hence, we must remember the areas of some usual shapes such as square, rectangle, circle, etc. The area of a square is equal to the square of their side, the area of a rectangle is its length times breadth and the area of the circle is pie $\left( \pi \right)$ times the square of the radius of the circle.