Question

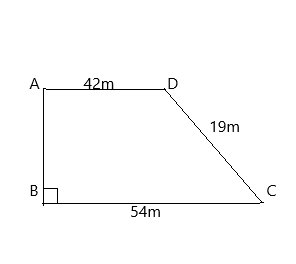
The length of the fence of a trapezium- shaped field ABCD is 130m and the side AB is perpendicular to each of the parallel sides AD and BC. If BC = 54m, CD = 19m and AD = 42m, find the area of the field?

Answer 1

Hint: In order to solve the question, first we will find the side AB of a trapezium using the perimeter of a trapezium which is equal to the length of the fence. Then we know that AB is the height of the trapezium by using the formula of area of trapezium i.e. \[\dfrac{1}{2}\left( a+b \right)\times h\], substituting the values in this formula we will get the required area of the field.

Formula used:
Area of the trapezium =\[\dfrac{1}{2}\left( a+b \right)\times h\], where ‘a’ and ‘b’ are the two parallel sides and ‘h’ is the height is of the trapezium.

Complete step by step solution:
We have given that,
A trapezium-shaped field ABCD having the sides AB, BC, CD and AD.
Sides having the measure of;
BC = 54m
CD = 19m
DA = 42m
It is given that,
The length of the fence of a trapezium-shaped field = 130m.
Now,
Perimeter of a trapezium shaped field = sum of all the sides of a trapezium
As we know that,
The length of the fence of a trapezium-shaped field is equal to the perimeter of the trapezium-shaped field.
Therefore,
Perimeter of a trapezium shaped field = sum of all the sides of a trapezium = length of the fence
Thus,
AB + BC + CD + DA = length of the fence
Substituting the values from the above, we get
AB + 54m + 19m + 42m = 130m
Adding the numbers, we get
AB + 115m= 130m
Therefore,
AB = 15m
Now,
As we know that AB is perpendicular to the side BC.
Thus, AB is the height of the trapezium.
Now,
Area of the trapezium = \[\dfrac{1}{2}\left( a+b \right)\times h\]
Where, ‘a’ and ‘b’ are the two parallel sides which are of the measure 54m and 42m and ‘h’ is the height is of the trapezium which is equal to AB = 15m.
Substituting the value, we get
Area of the trapezium = \[\dfrac{1}{2}\left( 54+42 \right)\times 15\]
Solving the above, we get
Area of the trapezium = \[\dfrac{1}{2}\left( 96 \right)\times 15=48\times 15=720{{m}^{2}}\]

Therefore,
Area of the field = \[720{{m}^{2}}\]
Hence, this is the required answer.

Note: In order to solve the given question, students need to know about the concept of trapezium and its properties. A trapezium of a quadrilateral having four sides from then two parallel sides of unequal length and the other two are the non-parallel sides. The parallel sides of the trapezium are also said bases and the other non-parallel sides of the given trapezium is said to be the legs of the trapezium. Trapezium can also be known as trapezoid.