Question

The length of the diagonal of a square is \[8\,cm\]. How long are the sides of the square?

Answer 1

Hint: In order to determine the length of the sides of the square, first we will draw a square, and assume $ x $ be the length of the sides of the square with the diagonal $ d = 8\;cm $ . Then, we will apply Pythagoras theorem to one of the triangles, where the two shorter sides of the triangle are the sides of the square, each one has length of $ x $ and the hypotenuse is the diagonal of the square. Rearrange the obtained equation and by evaluate and determine the value of $ x $ , which will be the length of the sides of the square.

Complete step-by-step answer:
It is given that the length of the diagonal of a square is \[8\,cm\].
We need to determine the length of sides of the square.

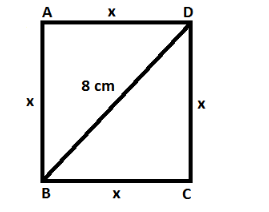
In general, diagonal $ d $ forms a triangle with adjacent sides $ a $ . Since this is a square we know it is a right triangle and we can use Pythagorean Theorem to determine the length of $ d $ . $ d $ is the hypotenuse and sides of the square is considered as the sides of the triangle in Pythagoras theorem.
Now, let $ x $ be the length of the sides of the square.
Consider the triangle $ ABD $ ,
By Pythagoras theorem,
 $ A{B^2} + A{D^2} = B{D^2} $
 $ {x^2} + {x^2} = {8^2} $
 $ 2{x^2} = 64 $
 $ {x^2} = \dfrac{{64}}{2} $
 $ {x^2} = 32 $
 $ x = \sqrt {32} $
 $ x = 4\sqrt 2 $
 $ x = 4 \times 1.414 $
Hence, $ x = 5.65\,cm $
Therefore, the length of sides of the square is $ 5.65\,cm $ .
So, the correct answer is “ $ 5.65\,cm $ ”.

Note: Diagonal is a line segment that joins two non-neighboring vertices. Each quadrilateral has two diagonals, a square too. Its diagonals are equal in length, perpendicular bisectors of each other and bisectors of square angles.
Each diagonal divides the square into two congruent isosceles right triangles. Such triangles have a half of the area of a square, its legs are the sides of the square and hypotenuse equals to the length of the diagonal of a square.
We can also determine the area of the square using the diagonal of the squares. The formula that can be used is, $ Area\,of\,the\,square = \dfrac{1}{2} \times {d^2}\,sq.uts $ , where $ d $ is the length of diagonal of the square.