Question

The length of the arc of a sector having central angle 90 degrees and radius 7cm is:
(a) 22cm
(b) 44cm
(c) 11cm
(d) 33cm

Answer 1

Hint: For finding the length of the arc of a circle we need to use the formula $R\theta $ , where R is the radius of the circle and $\theta $ is the angle subtended by the arc at the at the centre of the circle take in radians. So, for the above question R is 7 cm and convert $90{}^\circ $ to radians to get the value of $\theta $ .

Complete step-by-step answer:
Let us start by drawing a representative diagram of the situation given in the question for better understanding.

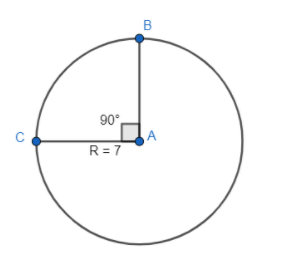
Now let us first convert $90{}^\circ $ to radians. We know that $180{}^\circ ={{\pi }^{c}}$ . If we divide both sides of this relation by 2, we get
$\dfrac{180{}^\circ }{2}=\dfrac{{{\pi }^{c}}}{2}$
$\Rightarrow 90{}^\circ =\dfrac{{{\pi }^{c}}}{2}$
So, $\theta $ for the above question is equal to $\dfrac{\pi }{2}$ .
Now we know that the length of the arc of a circle we need to use the formula $R\theta $ , where R is the radius of the circle and $\theta $ is the angle subtended by the arc at the at the centre of the circle taken in radians.
$arc\left( BC \right)=R\theta =7\times \dfrac{\pi }{2}$
Now we will put the value of $\pi =\dfrac{22}{7}$ .
$arc\left( BC \right)=7\times \dfrac{\pi }{2}=7\times \dfrac{22}{7\times 2}=11cm$
Therefore, the answer to the above question is option (c).

Note: If you want you can solve the question using the fact that the angle subtended by the whole circle at the centre is $360{}^\circ $ , so $90{}^\circ $ would be subtended by one fourth of the whole perimeter of the circle. Therefore, one fourth of the perimeter of the circle is the answer. Also, remember the value of $\pi $ you choose out of the two values $3,14\text{ and }\dfrac{22}{7}$ decides the complexity of the calculations.