Question

The length of second’s hand in a watch is 1cm. The change in velocity of its tip in 15 seconds is:
$\text{A.}\quad Zero$
$\text{B.}\quad \dfrac{\pi}{30\sqrt2} cm/s$
$\text{C.}\quad \dfrac{\pi}{30} cm/s$
$\text{D.}\quad \dfrac{\pi\sqrt2}{30 } cm/s$

Answer 1

Hint: There are majorly two types of quantities, scalar and vector quantities. All the quantities are divided into these two categories. Scalar quantities are those quantities, which have only magnitude eg – mass, speed, pressure, etc. Vector quantities are those which have both magnitude and directions eg – weight, velocity and thrust. For instance, speed is a scalar quantity and velocity is a vector quantity.

Formula used:
Change in velocity = $\vec v_2 - \vec v_1$

Complete answer:
How do we measure scalar quantity?
Like mass is a scalar quantity, hence can be measured by the scalar sum (normal sum) of individual mass.
How do we measure vector quantity?
Like velocity is a vector quantity, hence can be measured by the laws of vector addition. In general to get change in velocity, we need to do vector subtraction of the velocities at the two points.
Now, second’s hand takes 60 seconds for full rotation i.e. $360^\circ$
It will take 1 second for $\dfrac{360^\circ}{60}= 6^\circ$
So in 15 seconds, it will turn $15\times 6^\circ = 90^\circ$
Also the speed with which it rotates is:
Speed = rate of change of distance
It makes full rotation in 60 sec means it’s tip travels $2\pi R$(circumference) in 60 seconds.
Hence speed = $\dfrac{2\pi 1}{60} =\dfrac{\pi}{30}cm/s$

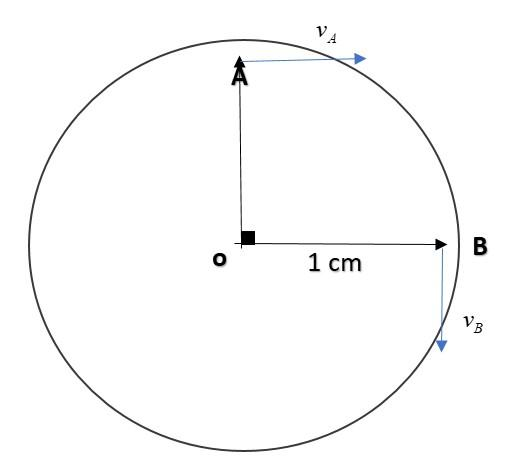
Now, from the diagram, we can see the two vectors ($\vec v_A ,\ \vec v_B$) are at $90^\circ$ and we need to find the magnitude of $\vec v_A - \vec v_B$.
Now, it could be done as follows:

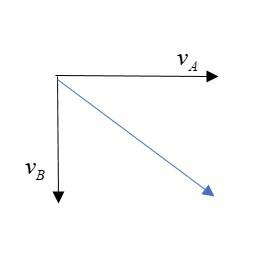
Where the angle between both velocity vectors is $90^\circ$ and the blue arrow will give the resultant of both velocities.
Change in velocity = $\sqrt{v_A^2 + v_B^2 - 2v_Av_B cos(90^\circ) }$
As $cos (90^\circ) = 0$ and magnitude of both velocities is same (v, say) = $\dfrac{\pi}{30}cm/s$
Hence, change in velocities = $\sqrt{v^2 + v^2} = v\sqrt2 = \dfrac{\pi\sqrt2}{30}cm/s$
Thus, option D is correct.

Note: To calculate the change in a vector quantity, we can’t do it algebraically. We have to do it by vector subtraction. Also there is an important property of vectors that they can be displaced anywhere hence we placed the vectors with the angle between them and calculated the resultant.