Question

The length of diagonal of cube is $15\sqrt{2}cm$, then the length of its side is-
A) $30\sqrt{2}cm$
B) $5\sqrt{6}cm$
C) $5\sqrt{2}cm$
D) $30cm$

Answer 1

Hint: We have been given the length of diagonal of the cube. Use the formula that the diagonal of any cube is equal to $\sqrt{3}$ times the side of the cube. You will get the length of the side.

Complete step-by-step answer:
So the cube is a symmetrical three-dimensional shape, either solid or hollow, contained by six equal squares. The cube is the only regular hexahedron and is one of the five Platonic solids. It has $6$ faces, $12$ edges, and $8$ vertices.
The cube is also a square parallelepiped, an equilateral cuboid and a right rhombohedron. It is a regular square prism in three orientations, and a trigonal trapezohedron in four orientations.
The cube is dual to the octahedron. It has cubical or octahedral symmetry.
The cube is the only convex polyhedron whose faces are all squares.
Cube has its length, breadth and height equal to each other.
The Cube has all its faces in a square shape. In a cube All the faces or sides have equal dimensions.
The plane angles of the cube are the right angles. Each of the faces meets the other four faces.
Each of the vertices meets the three faces and three edges. The edges opposite to each other are parallel.
The basic difference between a cube and cuboid is that a cube has equal length, height and breadth whereas in cuboids these three may or may not be the same. The cuboid can also be called a right rectangular prism.
A cube has eleven nets (one shown above): that is, there are eleven ways to flatten a hollow cube by cutting seven edges. To color the cube so that no two adjacent faces have the same color, one would need at least three colors.
The cube is the cell of the only regular tiling of three-dimensional Euclidean space. It is also unique among the Platonic solids in having faces with an even number of sides and, consequently, it is the only member of that group that is a zonohedron (every face has point symmetry).
The cube can be cut into six identical square pyramids. If these square pyramids are then attached to the faces of a second cube, a rhombic dodecahedron is obtained (with pairs of coplanar triangles combined into rhombic faces).

Now we have been given the length of the diagonal of the cube is $15\sqrt{2}cm$.
So we know that the diagonal of a cube is equal to $\sqrt{3}$ times the side of the cube.
Let the side of the cube be $x$.

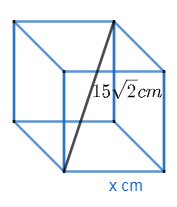
Here, $15\sqrt{2}cm=\sqrt{3}x$
So $x=\dfrac{15\sqrt{2}}{\sqrt{3}}=\dfrac{5\times \sqrt{3}\times \sqrt{3}\times \sqrt{2}}{\sqrt{3}}=5\sqrt{6}$
$x=5\sqrt{6}cm$
Here we get the length of the side is $5\sqrt{6} cm$.

Note: To find the length of the diagonal of a cube we can use pythagoras theorem as well. First we will find a diagonal of the square which is the base of the cube. Then again using pythagoras theorem we can find the diagonal of the cube.