
The length of chord of contact of the point (3, 6) with respect to the circle ${{\text{x}}^2} + {{\text{y}}^2} = 10$ is
$
{\text{A}}{\text{. }}\dfrac{{2\sqrt {70} }}{3} \\
{\text{B}}{\text{. 6}}\sqrt 5 \\
{\text{C}}{\text{. }}\sqrt 5 \\
{\text{D}}{\text{. }}\dfrac{{12}}{{\sqrt 5 }} \\
$
Answer
602.7k+ views
Hint:To find the length of the chord, we draw a perpendicular line segment from the center of circle O to the tangent, find the distance. Then using the Pythagoras theorem we find the length of the side AB. Twice the value of AB gives us the length of the cord.
Complete step-by-step answer:
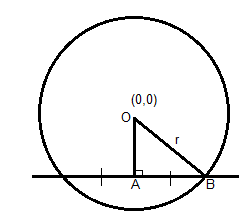
The chord of contact of the tangent from a point $\left( {{{\text{x}}_1},{{\text{y}}_1}} \right)$ to the circle equation${{\text{x}}^2} + {{\text{y}}^2} = {{\text{a}}^2}$, where a is the radius of the circle, is given by ${\text{x}}{{\text{x}}_1} + {\text{y}}{{\text{y}}_1} = {{\text{a}}^2}$.
So the equation of chord of the contact to the point (3, 6) with respect to the circle ${{\text{x}}^2} + {{\text{y}}^2} = 10$ is
3x + 6y = 10 -- (1)
And the radius of the circle is $\sqrt {10} $
We know the perpendicular distance from a point (h, k) to the line ax + by + c = 0 is given by
D = $|\dfrac{{{\text{a(h) + b(k) + c}}}}{{\sqrt {{{\text{a}}^2} + {{\text{b}}^2}} }}|$
Now the distance from the center of the circle O (0, 0) to the line 3x + 6y - 10 = 0, let the point it meets the line be A is given by
Hence OA = $|\dfrac{{{\text{3(0) + 6(0) - 10}}}}{{\sqrt {{3^2} + {6^2}} }}|{\text{ = }}\dfrac{{10}}{{\sqrt {45} }}$
Now from the figure OB is the radius of the circle, hence from the circle equation ${{\text{x}}^2} + {{\text{y}}^2} = 10$
We get radius a = OB = $\sqrt {10} $
Now we observe OA, OB and AB form a right angle triangle with the right angle at A. Hence the Pythagoras theorem for this triangle says ${\text{O}}{{\text{A}}^2} + {\text{A}}{{\text{B}}^2} = {\text{O}}{{\text{B}}^2}$.
$
\Rightarrow {\text{A}}{{\text{B}}^2}{\text{ = 10 - }}\dfrac{{100}}{{45}} = \dfrac{{350}}{{45}} \\
\Rightarrow {\text{AB = }}\dfrac{{\sqrt {70} }}{3} \\
$
Now length of the cord = 2×AB (as A is the midpoint of the cord).
∴Length of the cord =$\dfrac{{2\sqrt {70} }}{3}$. Hence Option A is the correct answer.
Note – In order to solve this type of questions the key is to know the formulae of the circle, tangent to a circle from a point and perpendicular from a point to a line. In a right angled triangle ABC, Pythagoras theorem states that In a right angles triangle sum of squares of other two sides is equal to square on the hypotenuse side i.e ${{\text{AB}}^2} + {{\text{BC}}^2} = {{\text{AC}}^2}$, where AC is the hypotenuse of the triangle. It is important to understand that the distance from the center of the circle to the chord is the perpendicular to it and it divides the chord equally.
Complete step-by-step answer:
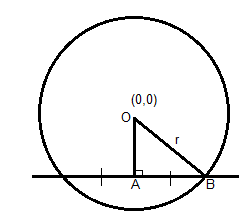
The chord of contact of the tangent from a point $\left( {{{\text{x}}_1},{{\text{y}}_1}} \right)$ to the circle equation${{\text{x}}^2} + {{\text{y}}^2} = {{\text{a}}^2}$, where a is the radius of the circle, is given by ${\text{x}}{{\text{x}}_1} + {\text{y}}{{\text{y}}_1} = {{\text{a}}^2}$.
So the equation of chord of the contact to the point (3, 6) with respect to the circle ${{\text{x}}^2} + {{\text{y}}^2} = 10$ is
3x + 6y = 10 -- (1)
And the radius of the circle is $\sqrt {10} $
We know the perpendicular distance from a point (h, k) to the line ax + by + c = 0 is given by
D = $|\dfrac{{{\text{a(h) + b(k) + c}}}}{{\sqrt {{{\text{a}}^2} + {{\text{b}}^2}} }}|$
Now the distance from the center of the circle O (0, 0) to the line 3x + 6y - 10 = 0, let the point it meets the line be A is given by
Hence OA = $|\dfrac{{{\text{3(0) + 6(0) - 10}}}}{{\sqrt {{3^2} + {6^2}} }}|{\text{ = }}\dfrac{{10}}{{\sqrt {45} }}$
Now from the figure OB is the radius of the circle, hence from the circle equation ${{\text{x}}^2} + {{\text{y}}^2} = 10$
We get radius a = OB = $\sqrt {10} $
Now we observe OA, OB and AB form a right angle triangle with the right angle at A. Hence the Pythagoras theorem for this triangle says ${\text{O}}{{\text{A}}^2} + {\text{A}}{{\text{B}}^2} = {\text{O}}{{\text{B}}^2}$.
$
\Rightarrow {\text{A}}{{\text{B}}^2}{\text{ = 10 - }}\dfrac{{100}}{{45}} = \dfrac{{350}}{{45}} \\
\Rightarrow {\text{AB = }}\dfrac{{\sqrt {70} }}{3} \\
$
Now length of the cord = 2×AB (as A is the midpoint of the cord).
∴Length of the cord =$\dfrac{{2\sqrt {70} }}{3}$. Hence Option A is the correct answer.
Note – In order to solve this type of questions the key is to know the formulae of the circle, tangent to a circle from a point and perpendicular from a point to a line. In a right angled triangle ABC, Pythagoras theorem states that In a right angles triangle sum of squares of other two sides is equal to square on the hypotenuse side i.e ${{\text{AB}}^2} + {{\text{BC}}^2} = {{\text{AC}}^2}$, where AC is the hypotenuse of the triangle. It is important to understand that the distance from the center of the circle to the chord is the perpendicular to it and it divides the chord equally.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Explain zero factorial class 11 maths CBSE

What is a periderm How does periderm formation take class 11 biology CBSE




