Question

The length of a side of an equilateral triangle is $ 21 $ cm. what would be the approximate area of the circumcircle of the above triangle?

Answer 1

Hint: The circumcircle is defined as the circle touching all the vertices of the triangle. Here we will draw the diagram with the given data and then will use the formula to get the area of the equilateral triangle and place the values and simplify the terms.

Complete step-by-step answer:
Equilateral of the triangle can be defined as the triangle with all the sides equal.

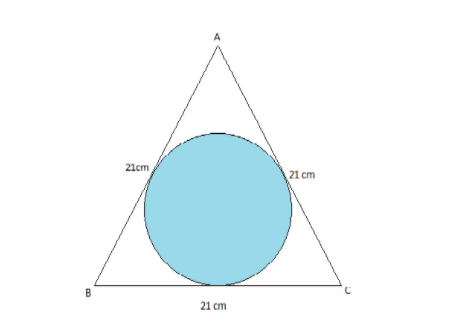
In the equilateral triangle, $\Delta ABC,\;{\text{A = B = C = 60}}^\circ $ and also given that measure of side $a = b = c = 21cm$
Radius of circumcircle (R) $ = \dfrac{a}{{2\sin A}} = \dfrac{b}{{2\sin B}} = \dfrac{c}{{2\sin C}}$
Place the given values in the above expression and $\sin 60^\circ = \dfrac{{\sqrt 3 }}{2}$
Radius of circumcircle (R)$ = \dfrac{{21}}{{2.\left( {\dfrac{{\sqrt 3 }}{2}} \right)}}$
Common factors from the numerator and the denominator cancel each other.
Radius of circumcircle (R)$ = \dfrac{{21}}{{\sqrt 3 }}$cm
Now, the area of the circumcircle of the equilateral triangle can be given by –
Area, $A = \pi {r^2}$
Where, r is the radius of the circumcircle
Place the value in the standard formula –
$A = \dfrac{{22}}{7} \times {\left( {\dfrac{{21}}{{\sqrt 3 }}} \right)^2}$
Simplify the above expression –
$A = \dfrac{{22 \times 21 \times 21}}{{7 \times 3}}$
Common factors from the numerator and the denominator cancel each other.
$A = 22 \times 21$
Find the products of the above terms –
$A = 462c{m^2}$
Hence, the area of the circumcircle of the triangle with $21cm$is $462c{m^2}$
So, the correct answer is “ $ 190.7325c{m^2} $ ”.

Note: Do not forget to write the appropriate unit after the solution. Also do not get confused with both the terms circumcircle and incircle of the triangle. Incircle can be defined when the circle is fitted inside the triangle or any regular polygon. Area of any figure is the space occupied by the object and is always measured in square units.