Question

The length of a rectangular rug is 2 feet more than its width. If the length of the rug is 8 feet, what is the area of the rug in square feet?
A) $16$
B) $48$
C) $66$
D) $80$

Answer 1

Hint:
We can obtain the relation between the length and width of the rug and write it as a mathematical equation. Then we can find the value of width by substituting the given value of length in the equation. Then we can find the area of the rug by multiplying the length and the width.

Complete step by step solution:

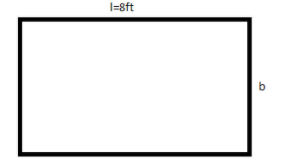
Let l be the length of the rectangle and b be the width of the rectangle.
We are given that the length of a rectangular rug is 2 feet more than its width. So, we can write it as,
$l = 2 + b$
We are given that the length of the rectangle is 8 feet. On substituting this value, we get,
$ \Rightarrow 8 = 2 + b$
On rearranging, we get,
$ \Rightarrow b = 8 - 2$
On simplification we get,
$ \Rightarrow b = 6$
Now we have the length and width of the rectangle. So, we can find the area by taking its product. It is given by,
$A = l \times b$
On substituting the values, we get,
$ \Rightarrow A = 8 \times 6$
After doing the multiplication, we get,
$ \Rightarrow A = 48$
Therefore, the area of the square rug is 48 square feet.

So, the correct answer is option B which is 48.

Note:
We must read the statement very carefully before writing the equation. We must keep in mind that, generally, the length will be greater than the width of a rectangle. We must take care of the units. As the length and breadth are given in feet, then the area will be in square feet. If we write the equation incorrect, we will get the breadth as 10 feet. Then we will get the area as $10 \times 8 = 80$ which is not the correct answer.